Радиофизические методы дистанционного зондирования земли, страница 14

Все результаты, которые были выше рассмотрены для сигналов в пространственной области имеют аналогичные представления и во времени, так как фаза и амплитуда ЭМВ содержат симметричные пространственно-волновым  (h,x) частотно-временные канонические переменные (ω,t). Поэтому, если зафиксировать координату или усреднить сигнал по пространственным переменным, то преобразования Фурье будут связывать между собой функции, зависящие от частоты и от времени:

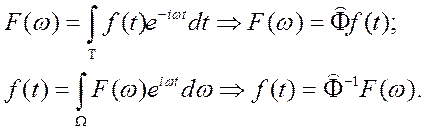                              (1.7.8)

Соответственно в реальности, аппаратура для детектирования сигналов в этом случае отличается от аппаратуры для получения пространственных картин. В практике современного зондирования используются методы, основанные как на частотных (спектральных) характеристиках сигналов, так и на их пространственных (структурных) составляющих. Все чаще полнота полученной информации зависит от применения интегрального подхода в сочетании с вычислительными математическими методами обработки полученных в эксперименте данных.                         

§ 8. ПРЕОБРАЗОВАНИЯ СВЕРТКИ. РАСПОЗНАВАНИЕ ОБРАЗОВ. ГОЛОГРАФИЯ.

Если сигнал представляет собой суперпозицию волн, идущих от различных объектов, то, как мы выяснили в предыдущем параграфе, происходит взаимная модуляция волн, которая при детектировании сигнала выглядит как своеобразное «искажение» и возникает проблема распознавания образов. Для выяснения возможностей разработки методик распознавания необходимо рассмотреть теоретически, каким образом происходит это искажение. Одна из самых важных теорем математического анализа – теорема о свертке функций –  во многом отвечает на этот вопрос.

При получении необходимого результата будем использовать вначале для простоты одномерное представление функций и их образов, а для наглядности выберем  пространственную форму преобразований Фурье.  Составим произведение фурье-образов двух функций , у которых значения переменных выбираются на оси Ox, причем y(x) = x – u, откуда следует, что dy = dx. Очевидно, что переменная  yпредставляет собой переменную x, смещенную на величину u. Так как при интегрировании в бесконечных пределах выбор начала отсчета не имеет значения, то образ функции f₂(y) совпадает с образом функции f₂(x).

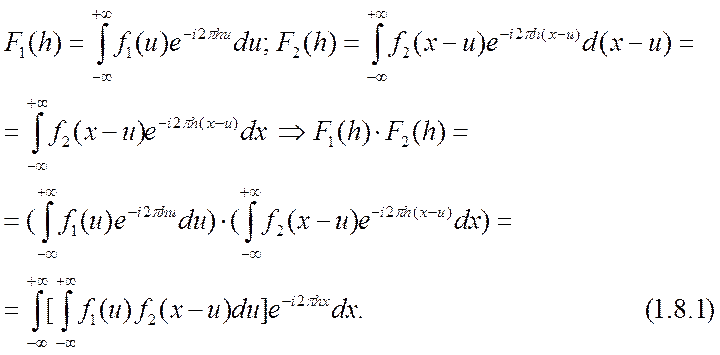
Выражение, записанное в квадратных скобках в последней строке равенств (1.8.1), содержит обе исходные функции и называется сверткой функций f₁  и  f₂ . Символически свертка записывается следующим образом:  . Результат вычислений (1.8.1) можно окончательно записать в виде

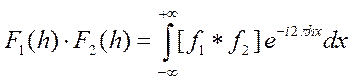.                                                (1.8.2)

Из равенства (1.8.2) следует, что фурье-образом свертки функций является произведение образов этих функций. Следствие, выделенное курсивом, составляет суть теоремы о свертке функций.

Для описания непрерывных и дискретных функций Дираком была введена обобщенная δ – функция, определяемая только своим фурье-образом:

 .

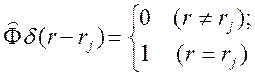Очень важным является случай свёртки дельта-функции с «хорошей» функцией f(x). Фильтрующее свойство дельта-функции может быть записано в виде свёртки:

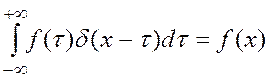. Или символически

                                          (1.8.3)

Таким образом, свёртка «хорошей» функции f(x) с дельта-функцией даёт исходную функцию f(x). Так как фурье-образом δ – функции является площадь, равная единице в точке r_i, то любую дискретную функцию g(r_j) можно представить в виде суммы δ – функций (с соответствующими «весовыми» множителями w_j), отличной от нуля только в точках r_j: 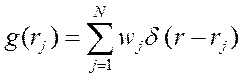 . Вычислительные задачи часто требуют замены непрерывной функции на дискретную и такую аппроксимацию также можно производить, используя дельта-функцию.

   Рис. 6. Геометрический подход к свертке функций

Геометрический смысл операции свертки легко понять, если произвести анализ подинтегрального выражения, которое представляет собой произведение функций в точках x и смещенных точках y = x – u. Очевидно, что одна функция при этом «сканируется» другой (рис. 6) или, если функции представляют собой некоторые «точечные» структуры, то свертка производит «размножение» точек одной структуры по точкам другой структуры.  Рассмотрим несколько примеров, связанных с применением свертки в проблеме распознавания образов.