4°. В газодинамике в силу наличия больших скоростей могут образовываться поверхности, при переходе через которые газодинамические функции (давление, скорость, плотность и другие) терпят разрыв, что означает возникновение ударных волн. Законы сохранения, очевидно, должны выполняться как в области определения непрерывных функций, так и на поверхности разрывов. Уравнения газодинамики в дифференциальной форме мы можем записать лишь для той части среды, в которой газодинамические функции и их первые производные остаются непрерывными. В общем случае уравнения газодинамики надо рассматривать в интегральной форме.
Выделим в жидкости (газе) некоторый движущийся объём V, ограниченный замкнутой поверхностью S, который состоит из одних и тех же частиц жидкости или газа. Объём V - произвольный. В частности, внутри V могут иметься поверхности, на которых терпят разрыв производные. Система уравнений газодинамики в интегральной форме имеет вид:
Закон сохранения массы:
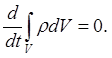 (1a)
(1a)
Закон сохранения импулъса:
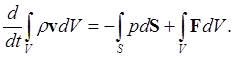 (4a)
(4a)
Закон сохранения энергии:
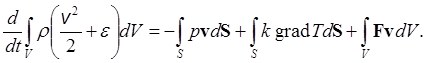 (5a)
(5a)
Покажем, как можно выводить уравнения газодинамики в дифференциальной форме, используя интегральную форму этих уравнений. Чтобы от интегральных уравнений перейти к эквивалентным им дифференциальным уравнениям, будем предполагать, что рассматриваемый объём не содержит поверхностей разрыва, т.е. все гидродинамические функции и их первые производные непрерывны.
В левой части каждого из интегральных уравнений стоят полные производные по времени. Мы не можем внести дифференцирование по t под знак интеграла, ибо "жидкий" объём зависит от времени. Поэтому выведем предварительно формулу для полной производной от интеграла по движущемуся объёму. Пусть
F = F(x,y,z,t) º F(г,t)
- любая ограниченная, интегрируемая по координатам и дифференцируемая по времени функция. Пусть за малый промежуток времени Dt объём V переходит в объём V' (соответственно поверхность S - в S').
По определению производной имеем
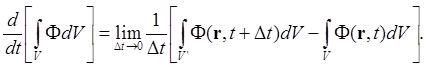
Обозначим F(r,t+Dt) через F1. Тогда
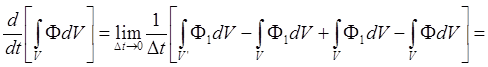
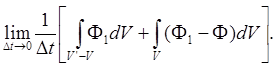
Частицы элемента dS поверхности S пройдут за время Dt расстояние vDt, где v - скорость движения соответствующего элемента поверхности. Траектории частиц при этом заполняют объём с основанием dS и образующими vDt, который равен dV = dSvDt. Поэтому для первого слагаемого справа получим
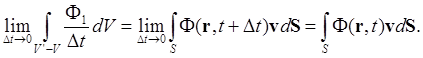
Найдём второе слагаемое:
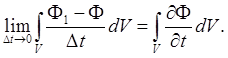
Окончательно получаем
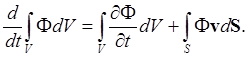
Используем теперь полученную формулу для вывода, например, уравнения непрерывности (1). Из уравнения (1а) имеем:
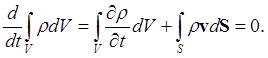
По теореме Гаусса-Остроградского (rv - дифференцируемая функция)
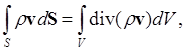
откуда
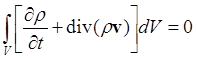
и следовательно, в силу произвольности объёма V
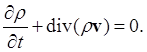
2. Уравнения акустики
Будучи выведенными из достаточно простых соображений, уравнения математической физики ведут к таким математическим следствиям, которые, если их перевести снова на язык физики, предсказывают явления, чрезвычайно далёкие от тривиальных. "Предвидение" результатов физических процессов возникает здесь как следствие математической обработки "общеизвестного". Это в полной мере относится к уравнениям газодинамики.
Уравнения гидродинамики - пример системы нелинейных дифференциальных уравнений в частных производных, которые трудно исследовать и трудно решать, особенно не для одномерных случаев.
Рассмотрим движение газа с малыми амплитудами и малыми скоростями. Будем предполагать также, что малы изменения плотности r и давления р:
r = r0 + r1, r1 << r0 (r0 - равновесная плотность);
р = р0 + р1, р1 << р0 (р0 - равновесное давление).
Пусть р = р(r). Тогда dp = p'(r0)dr, или p1 = а2r1 (р'(r0) > 0). Для адиабатического процесса в идеальном газе р = p0(r/r0)g и a2 = g(p0/r0), в чём легко убедиться, если взять логарифмическую производную:
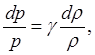
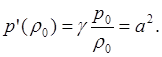
Произведём линеаризацию системы уравнений газодинамики
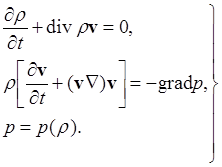 (7)
(7)
Предположим, что наряду с v, r1, p1 малы также и их производные по координатам и времени. Оставляя члены только первого порядка малости, систему уравнений (7) можно записать в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.