Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 13

Кроме самого уравнения, описывающего физический процесс, необходимо задать начальное состояние этого процесса (начальные условия) и режим на границе S той области D, в которой происходит процесс (граничные условия). Задание дополнительных условий связано с неединственностью решений дифференциальных уравнений. Действительно, даже для обыкновенных дифференциальных уравнений n-го порядка общее решение зависит от п произвольных постоянных. Для уравнений же в частных производных решение, вообще говоря, зависит от произвольных функций. Например, общее решение уравнения  имеет вид и(х, y) = f(x) + g(y), где f(x) и g(y) - произвольные дифференцируемые функции.

Поэтому, чтобы выделить решение, описывающее реальный физический процесс, необходимо задать дополнительные условия. Такими дополнительными условиями и являются "краевые" условия - начальные и граничные. Соответствующая задача называется "краевой задачей”.

2. Классификация краевых задач.

Различают три основных типа краевых задач для дифференциальных уравнений математической физики.

a) Краевая задача для гиперболических и параболических уравнений, когда решение ищется в некоторой ограниченной области D; задаются начальные и граничные условия. Такую задачу называют также смешанной.

b) Задача Коши для гиперболических и параболических уравнений. Решение ищется во всём пространстве, т.е. область D совпадает со всем пространством. Задаются начальные условия, граничные условия отсутствуют. Однако для того, чтобы решение имело смысл, требуют соответствующего поведения решения на бесконечности (например, его ограниченности).

c) Краевая задача для эллиптических уравнений. Задаются граничные условия, начальные условия отсутствуют.

Нам предстоит изучить методы решения сформулированных задач для уравнений гиперболического типа

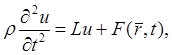                                                             (1a)

описывающих процессы колебаний; для уравнений параболического типа

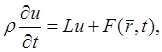                                                              (1b)

описывающих процессы распространения тепла, диффузии и вообще процессы переноса; для уравнений эллиптического типа

                                                                    (1c)

которые описывают соответствующие стационарные процессы. Здесь

Lu = div(k grad u) – qu (k = k(r) > 0, r = r(r) > 0).

Заметим, что различие в типах рассматриваемых уравнений тесно связано с различием физических процессов, описываемых этими уравнениями.

В качестве типичных примеров рассмотрим постановку некоторых задач для волнового уравнения и уравнения теплопроводности.

Из физических соображений следует, что для описания процесса колебаний струны необходимо дополнительно задать величины смещения и(х, 0) и скорости u_t(x, 0) струны в начальный момент времени (начальные условия), а также режим на концах струны (граничные условия).

Примеры граничных условий:

a)  если конец струны в точке х = x₀ закреплён;

b)  если конец струны (стержня) свободен.

c) Рассмотрим упругий стержень, к одному из концов которого приложена сила F(t). Для граничного элемента dx (Рис. 7) согласно второму закону Ньютона имеем

rdxu_tt = F(t) – s S, где s = Еe = Еи_x (E – модуль Юнга, e – относительное удлинение), т.е.

rdxu_tt(x^*, t) = F(t) – ESu_x(l – dx, t).

Пусть dx → 0. Тогда получаем

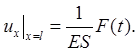
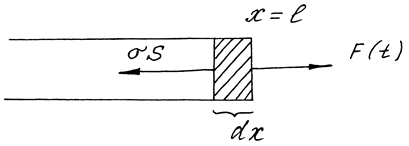
Рис. 7.

Для описания процесса распространения тепла необходимо задать начальное распределение температуры  в среде (начальное условие) и режим на границе этой среды (граничные условия).

Примеры граничных условий:

a) на границе S поддерживается заданное распределение температуры u₀(t):

b) на границе S поддерживается заданный поток тепла u₁(t):

c) на границе S происходит теплообмен по закону Ньютона:

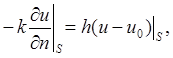
где h - коэффициент теплообмена, u₀ - температура окружающей среды.

Обобщим теперь для рассмотренных нами уравнений (1а), (1b) и (1с) постановку начальных и граничных условий. Если уравнение содержит u_t и не содержит производных более высокого порядка по времени, то надо задавать в начальный момент t = 0 функцию и(х, 0) = φ(х); если же в уравнение входит вторая производная по времени и_tt, то задаются в начальный момент функции