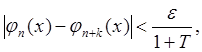
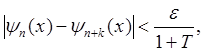
если п > N, k
- любое целое число, х -
любое число (из ограниченного интервала). Согласно полученной в теореме оценке
имеем ![]() где
где
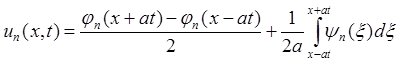
(для любых n > N, k - любое целое положительное число).
В силу критерия Коши (достаточность) это означает, что последовательность {un(x, t)} будет равномерно сходиться к некоторой функции u(x, t). При этом
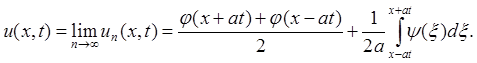
Эта функция называется обобщенным
решением задачи (1) - (2) в пространстве C(![]() ),
), ![]() -
некоторая конечная область на плоскости (x, t),
-
некоторая конечная область на плоскости (x, t),
![]()
Легко проверить, что она удовлетворяет начальным условиям. Полученная функция не зависит от выбора последовательности jn, yn. Замечательно, что в рассмотренном случае решение задачи Коши также дается формулой Даламбера (4).
§2. Решение краевых задач на полупрямой.
1. Однородные краевые задачи. Отражение волн на закрепленных и свободных концах.
Решим задачу
![]() (1)
(1)
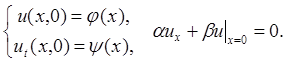 (2)
(2)
Эта задача представляет интерес в связи с изучением явлений отражения волн на границах. Кроме того, ее можно использовать как пропедевтический пример при выводе формулы Кирхгофа (см. §3.). Сведем задачу к предыдущей продолжением начальных данных на область х < 0. Ищем решение в виде
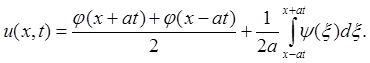
Если t - велико, то х – at < 0. Нужно доопределить j(х) и y(х) на отрицательную полуось. Имеем
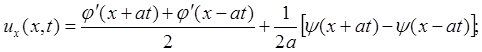
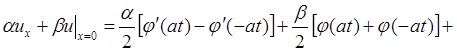
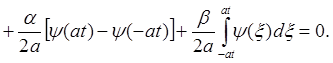 (3)
(3)
Функции j и y задаются независимо. Действительно, поставленную задачу, пользуясь линейностью уравнения, можно свести к двум аналогичным, в которых либо функция j(х), либо y(х) будет равна нулю. Поэтому естественно потребовать выполнения следующих условий:
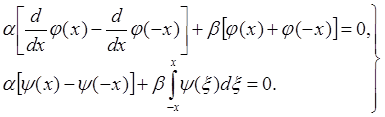 (4)
(4)
Мы положили в формуле (3) at = х. Перенесем теперь неизвестные функции в (4) в левую часть, предварительно продифференцировав второе уравнение:
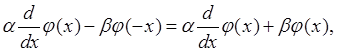
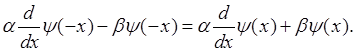
Для функций j и y мы получили одно и то же дифференциальное уравнение. Заметим, что это уравнение совпадает с уравнением для функции j(х) в аналогичной задаче по распространению тепла на полупрямой (см. гл. IV) Поэтому получаем:
а) ![]()
Заметим, что должны выполняться условия согласования
![]()
б) ![]()
![]()
в) ![]() Решаем линейное дифференциальное
уравнение с постоянными коэффициентами:
Решаем линейное дифференциальное
уравнение с постоянными коэффициентами:
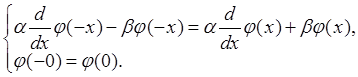
Продолжение y(х) производится аналогично.
С помощью метода продолжений удобно исследовать явления отражения волн от границ на свободном и закрепленном концах. В случае 1-ой краевой задачи (закрепленный конец) происходит отражение волны с сохранением величины отклонения, но с изменением его знака на противоположный (Рис. 15 "Изменение фазы на p").
а)
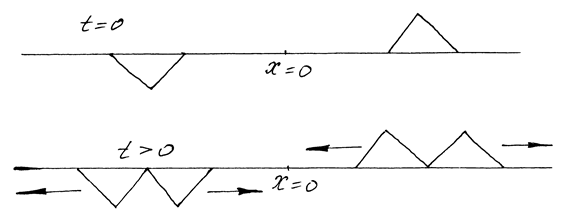
Рис. 15.
б) Здесь изменения фазы не происходит (b = 0).
2. Задача о распространении краевого режима на полупрямой.
Рассмотрим задачи:
1) ![]()
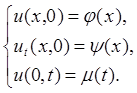
Поставленная задача является уже задачей с неоднородными граничными условиями. Мы заменяем ее двумя более простыми, первую из которых мы уже умеем решать: и = v + w.
I. ![]()
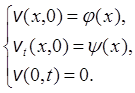
II. ![]()
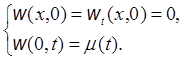
Единственная причина возникающего возмущения в задаче для w(x, t) - краевой режим: волна будет распространяться слева направо. Поэтому будем искать решение в виде
![]()
Имеем: ![]() Следовательно,
f(x) = C (C - некоторая постоянная).
Следовательно,
f(x) = C (C - некоторая постоянная).
![]() т.е.
т.е. ![]() при х
> 0.
при х
> 0.
Далее,
![]() т.е.
т.е. 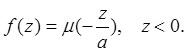
Таким образом,
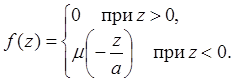
Это дает
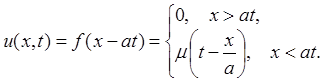
2) Задача для полубесконечного однородного стержня с заданной на конце силой F(t): utt = a2uxx, (0 < x, t < +∞).
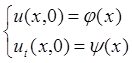
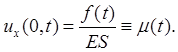
![]()
![]()
![]()
![]()
![]()
![]()
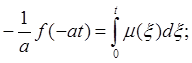
![]()
![]()
![]()
![]()
![]()
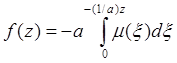
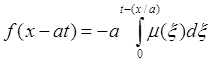
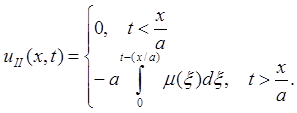
§3. Решение задачи Коши для трехмерного и двумерного волнового уравнения.
1. Решение задачи Коши для сферически-симметричного случая.
Рассмотрим задачу Коши для однородного волнового уравнения в 3-мерном пространстве:
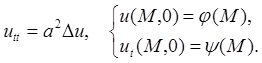 (1)
(1)
Получить решение задачи Коши для волнового уравнения в общем виде чрезвычайно важно, так как это уравнение описывает самые различные волновые процессы, встречающиеся в природе. И поэтому особенно приятно, что это тот редкий случай, когда решение задачи может быть выражено в виде явной формулы в реальном физическом пространстве (x, y, z, t).
а) Предварительно поставим задачу о нахождении решений однородного уравнения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.