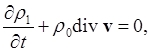Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 10

                                                               (7a)

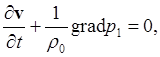                                                              (7b)

p₁ = a²r₁.                                                                       (7c)

Выведем, например, уравнение (7а). В рамках нашего приближения

div(rv) = v gradr₁ + r divv = v gradr₁ + r₁ divv + r₀ divv » r₀ divv.

Продифференцируем теперь (7b) по t, используя (7а) и (7c):

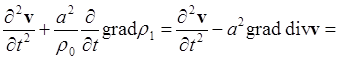
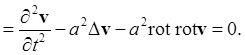
Согласно (7b) , так как rot gradp₁ = 0. Отсюда rot v(r,t) = rot v(r,0). Таким образом, для v получаем уравнение

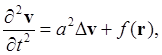 f(r) = a² rot rotv(r,0).

Пусть теперь . Согласно теореме Стокса это означает отсутствие вихрей. В самом деле, если бы при rotv = 0 вихри были (см. Рис. 4), то это противоречило бы теореме Стокса, так как при наличии вихря 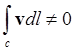, а с другой стороны по предположению .

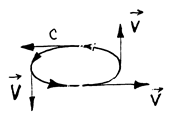
Рис. 4.

Таким образом уравнение для v будет иметь вид

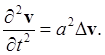                                                                       (8)

Продифференцируем теперь (7а) по t, используя (7b) и (7c):

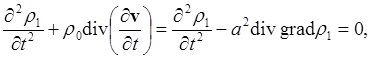
откуда

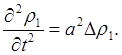                                                                    (9)

Так как p₁ = a²r₁, то для давления p₁ получаем также волновое уравнение.

Для оценки порядка малости скорости v перейдём к одномерному случаю. Как будет показано ниже (см. гл. III) и что легко проверить непосредственно, одномерное волновое уравнение (8) имеет решение вида

v = f(x – at), где f(x – at) - волна, бегущая слева направо со скоростью а (Рис. 5).

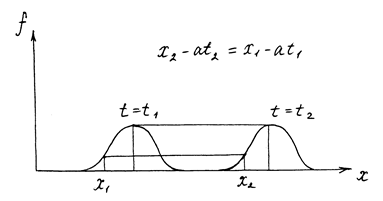
Рис. 5.

В соответствии с этим из (9) получаем (одномерный случай):

r₁ = F(x – at).

Согласно (7а) имеем

–aF' + r₀f' = 0, откуда

aF = r₀f + C.

Так как v = 0 при r₁ = 0, то С = 0 и следовательно

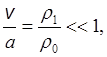
т.е. скорости v должны быть малы по сравнению со скоростью звука

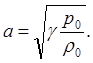
К этому же выводу можно прийти, рассматривая сдвиг поршня со скоростью v в однородном газе (Рис. 6):

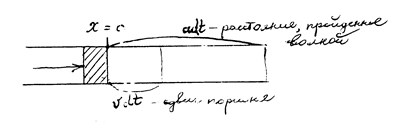
Рис. 6.

После сдвига поршня со скоростью v согласно закону сохранения массы имеем

М = r₀adt = r(а – v)dt.

Поэтому

(r – r₀)a = rv,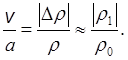 

Глава II

КЛАССИФИКАЦИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-ГО ПОРЯДКА И ПОСТАНОВКА ОСНОВНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

В предыдущей главе были выведены уравнения, к которым приводит математическое описание многих физических процессов. Было показано, что довольно широкий класс физических задач сводится к линейным дифференциальным уравнениям в частных производных 2-го порядка.

Например, было показано, что многие задачи механики (колебания струн, стержней, мембран), процессы распространения звука в однородной среде, процессы распространения электромагнитного поля описываются уравнениями вида

ru_tt = div (k gradu) + F(r,t).                                                          (1)

Процессы распространения тепла и диффузии частиц в среде описываются уравнением

ru_t = div (k gradu) – qu + F(r,t).                                                     (2)

Будем предполагать, что в уравнениях (1) и (2) r = r(r), k = k(r), q = q(r).

Для стационарных процессов, когда и = u(r), F(r,t) = F(r), уравнения (1) и (2) принимают вид

div (k gradu) – qu = – F(r).                                                          (3)

При k = const и q = 0 из уравнения (3) получаем уравнение Пуассона

Du = – f(r), 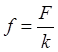.                                                                (4)

При f = 0 уравнение (4) переходит в уравнение Лапласа

Du = 0.                                                                           (5)

Уравнения (1) - (5) являются частными случаями дифференциальных уравнений 2-го порядка вида

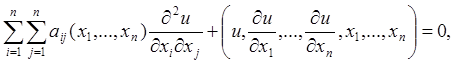                                   (6)

изучением которых мы в дальнейшем и ограничимся. Уравнение (6) называется уравнением 2-го порядка, линейным относительно старших производных. Частным случаем уравнения (6) является линейное уравнение

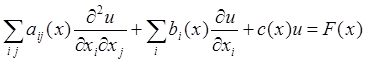                                            (7)

(здесь вместо х₁, х₂,..., x_n для краткости мы пишем х). При F(x) = 0 уравнение (7) называют линейным однородным уравнением.

Уравнений вида (6) очень много. Поэтому их желательно сначала систематизировать - привести к каноническому виду, а затем разрабатывать методы решения канонических уравнений. Классификацию уравнений (6) мы будем проводить относительно главной части