В последние годы появилось много работ, посвященных решению важных для практики некорректных задач. Академиком А.Н. Тихоновым был разработан в связи с этим метод регуляризации для построения приближенных решений таких задач (см. книгу А.Н. Тихонов, В.Я. Арсенин, Методы решения некорректных задач, М., Наука, 1979 г.)
В последующих главах будут рассмотрены основные методы решения для корректно поставленных задач математической физики - метод Фурье, метод функций Грина и метод характеристик.
Глава III
МЕТОД ХАРАКТЕРИСТИК
Одним из эффективных методов построения решений и исследования свойств решений уравнений в частных производных и систем таких уравнений является метод характеристик. На его основе строятся также численные методы решения систем гиперболических уравнений.
§1. Решение задачи Коши для одномерного волнового уравнения
1. Формула Даламбера. Область зависимости решения от начальных данных.
Требуется найти решение задачи Коши
(1)
(2)
непрерывное в области {– ∞ < х < ∞, t ≥ 0} вместе с первыми и вторыми производными.
Решение будем искать в виде суперпозиций прямой и обратной
бегущих волн (см. переход от х, t к x, h). Так
как 
то
(3)
Среди решений вида (3) найдем такое, которое удовлетворяет начальным условиям (2):
Мы получили два уравнения: одно - алгебраическое, другое - дифференциальное. Интегрирование дает:
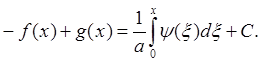
Отсюда находим
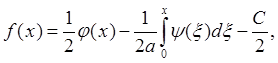
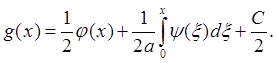
Заметим, что каждая из волн определяется неоднозначно. Однако для и(х, t) получаем
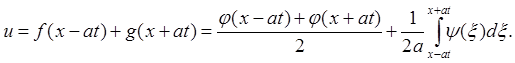(4)
Постоянная C сократилась. Мы получили формулу Даламбера. Метод получения решения называется методом бегущих волн, или методом характеристик.
Получив решение в явном виде, естественно исследовать его и найти физические следствия.
1) Пусть y(х)
= 0, а функция j(х)
имеет вид "горбика". Видно, что два горбика, каждый из которых при t
= 0 равен 
будут
расходиться в ± ∞ со скоростью а (колебаний не будет). Заметим, что при y(х)
≠ 0 первообразная также дает две волны F(x ± at).
2) Значение и в точке (x, t) зависит только от начальных данных в точках основания характеристического треугольника. Начальные условия вне основания не влияют на решение в точке (x, t) (см. Рис. 13).
3) Если начальные данные отличны от нуля лишь на некотором отрезке [a, b], то область зависимости решения от начальных данных будет ограничена характеристиками, проведенными через точки a и b и отрезком [a, b] (Рис. 14).
Рис. 13
Рис. 14.
2. Устойчивость решения. Обобщенное решение.
Теорема. Если функция j Î C2 y Î C1 (Ck - класс функций, имеющих непрерывные производные до k-го порядка включительно), то решение задачи (1) - (2) существует, единственно и выражается формулой Даламбера.
Решение непрерывно зависит от начальных данных в
следующем смысле: если 
то
Доказательство существования проводится путем подстановки решения в уравнение (проверка).
Для доказательства единственности рассматривают разность v = и1 – и2 и пользуются формулой Даламбера, что дает v = 0.
Непрерывная зависимость от начальных данных вытекает из формулы Даламбера:
или, что то же самое, если
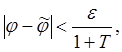
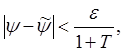то 
Таким образом, малым изменениям начальных данных соответствуют малые изменения решения задачи Коши.
В практических задачах начальные значения получаются в результате измерений. Доказанная теорема создает уверенность, что небольшие погрешности, допущенные при определении начальных значений, приводят к небольшим изменениям в решении. Эта теорема указывает также на один из возможных путей построения решения в случаях, когда начальные функции j(х) и y(х) не обладают соответствующими производными.
Пусть j Ï C2, y Ï C1 и пусть функции j и y не равны нулю на конечных отрезках и непрерывны. Аппроксимируем их равномерно функциями jn(х) Î C2 и yn(x) Î C1, например, полиномами (опираясь на теорему Вейерштрасса). Если заданы e и Т, 0 < t < T, тогда согласно критерию Коши найдется такое N(e), что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.