Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 7

Когда в проводах слева и справа от конденсатора течёт переменный ток, то в пространстве между пластинами конденсатора обязательно меняется электрическое поле. Значит, переменное электрическое поле можно рассматривать наравне с обычным током - движением заряженных частиц. Максвелл, высказавший эту точку зрения, сумел получить из неё важные следствия. Давно было известно, что электрический ток вызывает появление магнитного поля. Но если переменное электрическое поле подобно электрическому току, то переменное электрическое поле в пустоте тоже должно создавать переменное магнитное поле. Эта гипотеза Максвелла привела к замечательной симметрии между электрическим и магнитным полями. Фарадей экспериментально открыл, что изменение магнитного поля вызывает появление электрического поля. Максвелл умозрительно пришёл к предположению о существовании аналогичного явления, при котором изменение электрического поля вызывает появление магнитного поля. В результате этого предположения в правой части последнего из уравнений системы (1) появился член  и теория электрических и магнитных полей приобрела современный вид.

В случае вакуума j = 0, r = 0, e = 1, m = 1. Уравнения (1) тогда запишутся следующим образом:

div E = 0,                                                                       (1a)

div H = 0,                                                                      (1b)

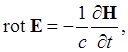                                                                  (1c)

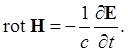                                                                  (1d)

Применим оператор rot к последней паре уравнений. Так как

rot rot a = grad div a – Dа,                                                           (2)

то принимая во внимание (1а) и (1b), получим

rot rot E = – DЕ, rot rot H =– DН.

В результате уравнения (1с) и (1d) перейдут в уравнения

 .

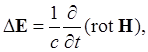
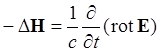Отсюда

 

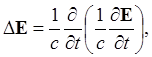
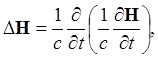
т.е.

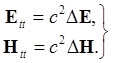                                                                      (3)

Таким образом, для каждой из компонент электрического и магнитного поля Е и Н мы получили трёхмерные волновые уравнения.

Из уравнений (3) видно, что скорость распространения электрических и магнитных полей в пустоте оказывается равной скорости света с (см. Глава III). Отсюда естественно последовало предположение, что свет и есть не что иное, как электромагнитные колебания. Кроме того, из уравнений (3) вытекает возможность существования электромагнитных колебаний любой длины волны, в том числе рентгеновских лучей и радиоволн.

Рассмотренный пример поучителен с точки зрения взаимоотношений теории и опыта: теория основывается на определённых данных опыта, но последовательное логическое и математическое развитие теории выводит за пределы того материала, который был положен в ее основу, приводит к новым предсказаниям^[2].

§4. Уравнения гидродинамики и акустики

1. Система уравнений гидродинамики

Чтобы описать состояние жидкости (газа) как сплошной среды, надо задать поле скоростей v(r,t) и какие-нибудь две термодинамические функции. Обычно задают давление p(r,t) и плотность r(r,t). Для нахождения функций, описывающих состояние движущегося газа, служит система уравнений газодинамики. Эта система представляет собой выраженные в математической форме фундаментальные законы природы: закон сохранения массы, импульса и энергии вещества.

1°. Закон сохранения массы, или количества вещества в заданном объеме, выражает уравнение непрерывности. Выделим в жидкости (газе) некоторый фиксированный объем V, ограниченный замкнутой поверхностью S. Пусть j = rv - вектор плотности потока жидкости. Тогда

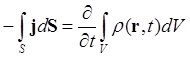
(dV - элемент объёма), откуда

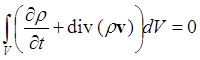
и следовательно,

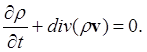                                                                  (1)

Уравнение (1) называется уравнением непрерывности. Оно свидетельствует о том, что изменение плотности r в данном элементе объема происходит за счет втекания (или вытекания) вещества в этот элемент.

2°. Перейдем теперь к выводу уравнения движения, называемого уравнением Эйлера. При выводе будем опираться на 2-ой закон Ньютона. Рассмотрим некоторый произвольный движущийся объем, ограниченный поверхностью S, внутри которого находятся одни и те же частицы жидкости или газа. К рассматриваемому "жидкому" объему могут быть приложены силы различных типов.