Физика \ Методы математической физики

Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 15

чтобы на его примере выяснить, какую роль играют характеристики в постановке краевых задач.

Для обыкновенного дифференциального уравнения второго порядка, написанного для функции y(х), задания значений y и y' в точке x0 вместе с самим дифференциальным уравнением достаточно, чтобы найти все высшие производные в точке x0 и тем самым построить решение вблизи точки x0 в виде ряда Тейлора.

По аналогии с обыкновенным дифференциальным уравнением второго порядка можно было бы ожидать, что для уравнения в частных производных (3) задача Коши, т.е. задание значений функции и(х, y) на некоторой кривой и ее первых производных (точнее, производной по направлению нормали к этой кривой, так как производная вдоль кривой фактически задана) - наиболее естественный вид граничных условий. Исследуем в связи с этим, достаточно ли задания на некоторой кривой х = x(s), y = y(s) значений функции и(х, y) и (Ñu)n, чтобы построить решение в виде ряда Тейлора вблизи кривой.

Зная в каждой точке кривой производные  и , т.е.  мы можем вычислить первые производные  и :

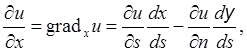
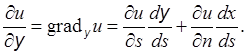
(направляющие косинусы единичного вектора нормали n суть ).

Исследуем теперь вопрос о нахождении вторых производных uxx, uyy, и uxy. Два уравнения для них получаем, дифференцируя известные нам первые производные вдоль кривой:

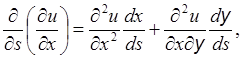
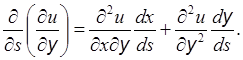
Третьим уравнением является исходное уравнение (З):

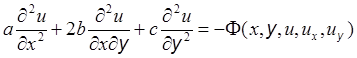
(в правой части стоит известная функция). Эти три неоднородных уравнения нельзя решить относительно вторых частных производных, если детерминант системы равен нулю, т.е.

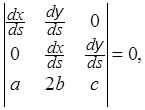
или

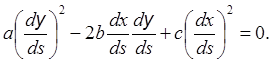                                                     (4)

Мы получили уравнение, совпадающее с уравнением для характеристик (8) из §2

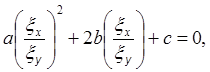
так как 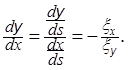В каждой точке уравнение (4) определяет, вообще говоря, два характеристических направления. Кривые в плоскости хy, наклон которых в каждой точке совпадает с характеристическими направлениями, и являются характеристиками дифференциального уравнения в частных производных.

Таким образом, вторые производные определяются всюду, кроме точек, где "краевая" кривая, на которой заданы граничные условия, является касательной к характеристикам. Дальнейшим дифференцированием можно получить аналогичную систему уравнений для производных третьего и более высокого порядка. Условие для их разрешимости будет содержать тот же детерминант. Следовательно, рассмотренные дополнительные условия определяют решение, если "краевая" кривая нигде не касается характеристики.

Для гиперболических уравнений, когда b2 > ас, мы имеем две вещественных характеристи-ки. Характеристики в данном случае - это кривые, вдоль которых распространяется информация о решении (см. гл. V).

Пример 1. Рассмотрим простейшее гиперболическое уравнение

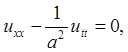                                                                    (5)

для которого а = 1, b = 0,  Характеристическое уравнение (4) для него имеет вид

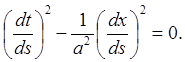
Характеристики представляют собой прямые линии:

Характеристики гиперболического уравнения образуют "естественную" систему координат. В новых координатах x, h уравнение (5) имеет вид

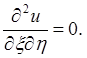
Его решение очевидно:

т.е.

где f и g - произвольные дифференцируемые функции.

Пусть нам известна вдоль отрезка АВ (Рис. 12) функция

и ее нормальная производная

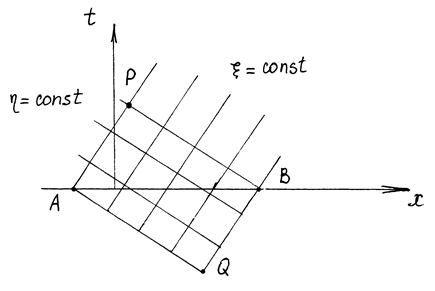
Рис. 12.

Тогда мы можем найти вдоль всего отрезка функции f(x) и g(х) из системы уравнений:

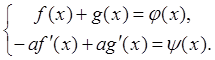
Значения f(x) вдоль отрезка АВ определяют f(x) вдоль всех характеристик x = const, которые пересекаются с АВ. Аналогично значения g(х) определяют g(h) вдоль всех кривых h = const, которые пересекаются с АВ. Как f(x), так и g(h), а, следовательно, и u(x, t) определяются в той области APBQ, где пересекаются оба типа характеристик.

Результаты, полученные для этого простого примера, могут быть обобщены на произвольные гиперболические уравнения, когда функция и и ее производная по нормали заданы на некоторой дуге, а характеристики не являются прямыми линиями.

Скачать файл