Если в некоторой точке х разрезать струну на две части, то действие правой части на левую выразится в виде силы Т(x,t). В рамках нашего приближения величина силы натяжения струны Т(x,t) (Рис. 1) не должна зависеть от времени:
T(x,t) = Т(х).
Запишем теперь уравнение движения точек струны, используя второй и третий закон Ньютона. Пусть r(х) - линейная плотность струны в точке x, F(x,t) - величина линейной плотности внешних сил, направленных перпендикулярно оси х. На элемент струны (х,х + dx) действуют (Рис. 2) силы натяжения T(x + dx), – T(x) и внешняя сила F(x,t)dx. Векторная сумма этих сил должна быть равна произведению массы рассматриваемого участка r(x)dx на ускорение a:
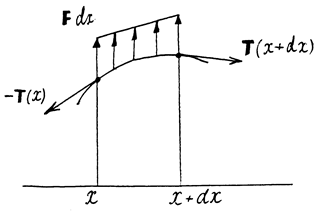
Рис. 2
T(x + dx) – T(x) + Fdx = r dx a. (1)
Спроектируем полученное векторное равенство на оси х и и:
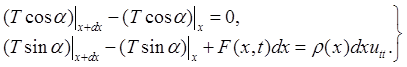(2)
В нашем приближении
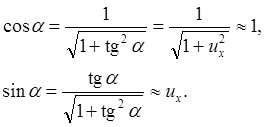
Поэтому из (2) имеем
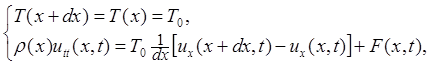
откуда при dx ® 0 получим
r(x)utt = T0uxx + F(x,t). (3)
Это и есть уравнение малых поперечных колебаний струны. Оно было получено нами, как говорят, на физическом уровне строгости.
Приведем еще один вывод уравнения (3), который является более общим[1]. Он основан на применении 2-го закона Ньютона в интегральном виде. Этот вывод может быть полезен, например, в случае, когда к струне приложена сосредоточенная сила.
Рассмотрим конечный участок струны (x1,x2). Изменение количества движения участка Dx = х2 – х1 за время Dt = t2 – t1 равно импульсу действующих сил. Проекция соответствующего векторного равенства на ось и дает:
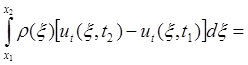
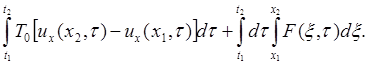
Для перехода к дифференциальному уравнению используем теорему о среднем
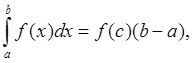cÎ[a,b], (4)
и формулу Лагранжа для конечных приращений
F(b) – F(a) = F' (c)(b – a), которую легко получить из (4) при
f(x)=F'(x). (5)
Если предположить существование и непрерывность вторых производных функции u(x,t), то с помощью (4) и (5) получим
r(x1)utt(x1,t1)DtDx = T0uxx(x2,t2)DxDt + F(x3,t3)DxDt, где
x1,x2,x3 Î [x1,x2], t1,t2,t3 Î [t1,t2].
После деления на DxDt и перехода к пределу при Dx ® 0, Dt ® 0, снова придем к уравнению (3).
Если плотность струны постоянна, т.е. r(х) = r0 уравнение колебаний струны можно записать в виде
utt = a2uxx + f(x,t), (6)
где а2 = 
, f = 
.
Уравнение (6) называют одномерным волновым уравнением.
Уравнение вида (6) описывает, например, также малые продольные колебания
однородного упругого стержня.
Аналогично с помощью 2-го закона Ньютона выводится уравнение малых поперечных колебаний мембраны. Формально оно получается из (6) заменой иxx ® иxx + uyy, что приводит к двумерному волновому уравнению
utt = a2(uxx + uyy) + f(x,y,t), где и = u(x,y,t) - смещение, перпендикулярное плоскости мембраны (x,y), в момент времени t.
Замечание. Полезно уметь выводить волновые уравнения с помощью вариационных принципов (см. например, Г.Е.Шилов, Математический анализ, Специальный курс, гл. III, a также [4]).
§2. Уравнения теплопроводности и диффузии
Процесс распространения тепла в некоторой сплошной среде может быть охарактеризован температурой u(r,t), являющейся функцией радиус-вектора г и времени t. Считая среду изотропной, обозначим через r(r), c(r), k(r) плотность, удельную теплоёмкость и коэффициент теплопроводности соответственно.
Пусть, далее, F(r,t) - интенсивность тепловых источников в точке г в момент t.
Подсчитаем баланс энергии в произвольном объеме V,
ограниченном фиксированной поверхностью S, для двух близких моментов
времени t и t + Dt.
За счет источников тепла в объеме V за время Dt возникает количество энергии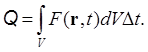 
Эта
энергия частично выходит через поверхность (Q1),
а остаток ее расходуется на подогрев вещества (Q2). Количество тепла,
вытекающее через элемент поверхности dS в единицу времени, согласно
закону Фурье равно
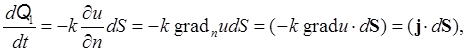
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.