Заметим, что уравнение (4) есть условие равенства нулю
коэффициента ã, определяемого формулой (5) из §2. Поэтому если
"краевая" кривая является характеристикой x = x(x,
t), то переходя к новым независимым переменным x = x(x,
t), h = h(x, t) в уравнении (3), мы
получаем из него соотношение между и и ![]() (что
соответствует
(что
соответствует ![]() ) вдоль характеристики, которое
не позволяет задавать функцию и ее нормальную производную на характеристике
независимым образом. Свобода задания начальных данных
в этом случае снижается.
) вдоль характеристики, которое
не позволяет задавать функцию и ее нормальную производную на характеристике
независимым образом. Свобода задания начальных данных
в этом случае снижается.
Для эллиптических уравнений, когда b2 < ас, вещественных характеристик не существует. Здесь информация о решении как бы "диффундирует" внутрь области от замкнутой границы, на которой задаются условие Дирихле или Неймана, или их комбинации.
Рассмотрим, наконец, параболические уравнения, когда b2 = ас. Эти уравнения описывают процессы переноса и с физической точки зрения характерны своей необратимостью по времени. Так например, для уравнения теплопроводности или диффузии решение находится для будущих моментов времени. Решение для прошедших моментов найти нельзя (не будет устойчивости). Если время движется вперёд, то процесс диффузии сглаживает особенности, если назад - то особенности возникают, и без дополнительной информации решение продолжить невозможно.
Пример 2. Уравнение теплопроводности
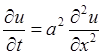
приводит к уравнению характеристик ![]() т.е. характеристики представляют собой
прямые t = const, параллельные оси х. Задача определения
температуры для t > 0 по начальным значениям и(х, 0)
представляет собой задачу с данными на характеристике. Именно поэтому здесь
задается в качестве начального условия только одна функция, хотя уравнение
теплопроводности второго порядка. Поставленная задача для уравнения
теплопроводности по существу не является задачей Коши, хотя такое название в
литературе ей часто присваивается (и мы тоже его будем придерживаться).
т.е. характеристики представляют собой
прямые t = const, параллельные оси х. Задача определения
температуры для t > 0 по начальным значениям и(х, 0)
представляет собой задачу с данными на характеристике. Именно поэтому здесь
задается в качестве начального условия только одна функция, хотя уравнение
теплопроводности второго порядка. Поставленная задача для уравнения
теплопроводности по существу не является задачей Коши, хотя такое название в
литературе ей часто присваивается (и мы тоже его будем придерживаться).
§4. Корректность постановки задач математической физики
1. Существование и единственность решения, непрерывная зависимость решения от исходных данных.
Поскольку задачи математической физики описывают реальные физические процессы, то математическая постановка этих задач должна удовлетворять следующим естественным требованиям:
а) Решение должно существовать в каком-то классе функций M1. Дополнительных данных не должно быть слишком много, они не должны противоречить друг другу, среди них не должно быть несовместных. Другими словами, задача не должна быть "переопределена". Вопрос существования снимается, если решение построено. Обычно существование решения следует из самой физической постановки задачи.
б) Решение должно быть единственным в некотором классе функций М2. Дополнительных данных должно быть достаточно для выделения однозначного решения.
в) Решение должно непрерывно зависеть от исходных данных задачи (начальных и граничных условий, свободного члена, коэффициентов уравнения), то есть быть устойчивым.
Требования непрерывной зависимости решения обусловливаются тем обстоятельством, что исходные данные определяются из эксперимента приближенно и поэтому нужно быть уверенным в том, что решение задачи не будет существенно зависеть от погрешностей измерений.*)
Задача, удовлетворяющая поставленным требованиям, называется корректно поставленной, а соответствующее множество функций M1 ∩ М2 - классом корректности.
Нахождение корректных постановок задач математической физики и методов построения их решений (точных или приближенных) составляет основное содержание курса "Уравнения математической физики"
2. Примеры некорректно поставленных задач.
1) Пример Адамара (задача Коши для уравнения Лапласа)
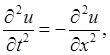
![]()
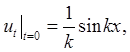
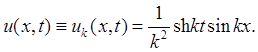
Если k → ∞, то ![]() но
но ![]()
В то же время уравнение имеет решение и ≡ 0, соответствующее нулевым начальным данным.
2) Найти, какое начальное распределение температур при t = Т < 0 соответствовало профилю температур при t = 0.
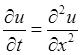
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.