Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 19

которые обладают центральной симметрией относительно некоторой точки М, т.е. решений вида и = u(r, t), где r - расстояние от рассматриваемой точки (x, y, z) до точки М, которая выбрана в качестве начала координат. В этом случае волновое уравнение сводится к одномерному уравнению для функции v = ru. Действительно, так как

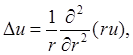
то вводя функцию v = rи, находим

Если функция u(r, t) ограничена при r = 0, то v(0, t) = 0. Поэтому задача Коши для уравнения  с начальными данными u(r, 0) = j(r), u_t(r, 0) = y(r) сводится к задаче о колебаниях струны (0 ≤ r < ∞) с закрепленным концом r = 0:

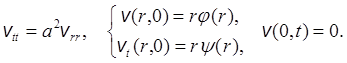
b) Для решения задачи (1) введем вспомогательную функцию

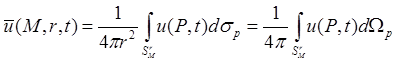                                         (2)

которая представляет усреднение искомого решения по сфере  радиуса r с центром в точке М. Сначала решим задачу для  а затем, применяя теорему о среднем и устремляя r к нулю, получим

Чтобы поставить задачу для функции  докажем лемму.

Лемма.

                                                                      (3)

Здесь в левой части лапласиан, входящий в (1), берется по координатам точки М в исходной системе координат, а в правой части - по r, причем начало координат находится в точке М. Пусть - шар радиуса r с центром в точке М. Тогда, используя инвариантность оператора Лапласа D относительно трансляций и применяя формулу Гаусса-Остроградского, получаем:

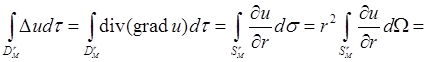
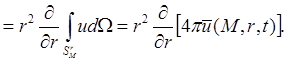
С другой стороны, по определению объемного интеграла по шаровой области имеем:

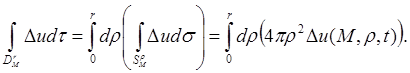
Сравнение полученных выражений дает

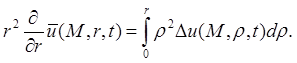
Последнее равенство справедливо при любых r. После дифференцирования его по r получаем

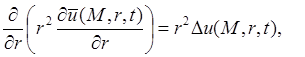т.е.

2. Формула Кирхгофа.

Осредним уравнение (1) и начальные условия по формуле (2). Согласно лемме  т.е. осредненное решение удовлетворяет волновому уравнению при любом r > 0.

Сделаем замену

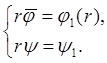
Для функции v = v(r, t) получаем задачу: v_tt = a²v_rr,

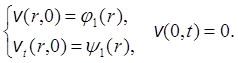
Пусть (см. §2, п.1)

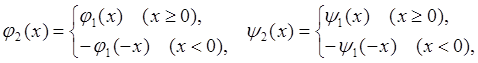
Тогда

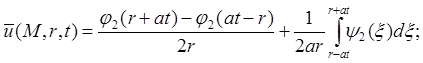
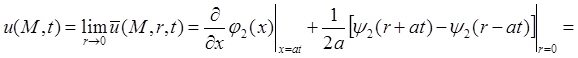
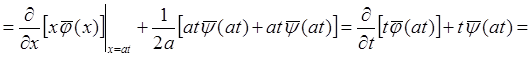
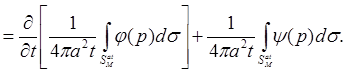
Мы получили формулу Кирхгофа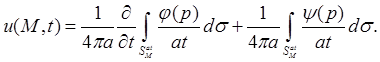:[4]

                                          (4)

З*. Двумерный случай.

Из формулы Кирхгофа можно получить также решение задачи Коши для однородного волнового уравнения в двумерном пространстве:

В самом деле, если в формуле (4) функции j(p) и y(p) не зависят от переменной z то интегралы по поверхности сферы  можно свести к интегралам по экваториальному кругу этой сферы  лежащему в плоскости (x, y) (Рис. 16). Интеграл по верхней половине сферы  равен

где g - угол между нормалями к плоскости (x, у) и к сфере  в точке Р. Очевидно,

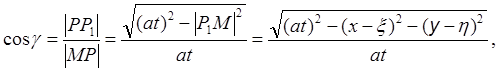
здесь x, h - координаты точки P₁, являющейся проекцией точки P на плоскость (х, у); (x, у, 0) - координаты точки наблюдения M.

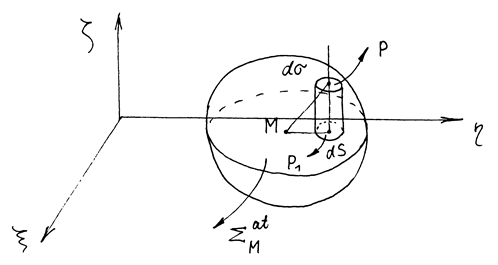
Рис. 16

Поэтому

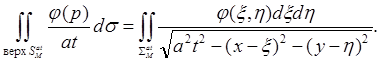
Для нижней половины сферы аналогично находим:

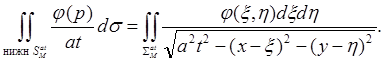
§4. Решение неоднородных задач. Принцип Дюамеля

1. Неоднородное уравнение

Нами было решено однородное волновое уравнение. Поэтому для неоднородного уравнения

с нулевыми начальными условиями по принципу Дюамеля будем иметь

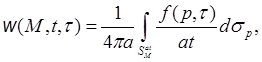
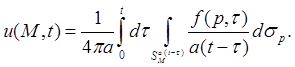
Замена переменных интегрирования:

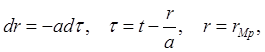
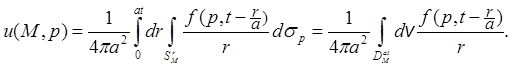
Пусть например,

Тогда

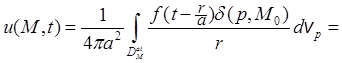
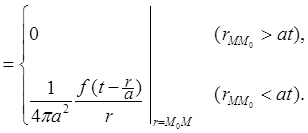
Решение имеет простой смысл: от точки M₀ идет со скоростью a сферическая волна, амплитуда которой пропорциональна  Этот факт легко понять из физических соображений. Известно, что плотность энергии в волне зависит от квадрата амплитуды волны. По мере того как волна разбегается, ее энергия расплывается на все большую и большую площадь, пропорциональную квадрату радиуса волны. Если полная энергия сохраняется, то плотность энергии должна убывать как  а амплитуда - как

Продолжение следует.