Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 6

где j = – k gradu есть вектор плотности потока тепла, n - единичный вектор внешней нормали, dS = ndS - так называемый вектор площадки (Рис. 3).

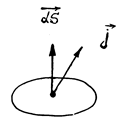
Рис. 3

Следовательно,

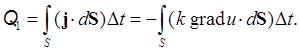
На подогрев вещества за время Dt расходуется количество энергии

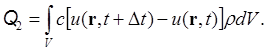
По закону сохранения энергии Q = Q₁ + Q₂, откуда после перехода к пределу при Dt ® 0 получим

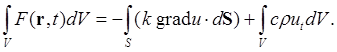
По теореме Гаусса-Остроградского

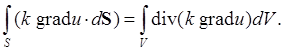
Мы предполагаем что поверхность S - кусочно гладкая, т.е. состоит из конечного числа кусков с непрерывно меняющейся на них касательной плоскостью. Отсюда

                                                  (1)

Будем предполагать, что все входящие в подинтегральнное выражение функции - непрерывны. Так как равенство (1) справедливо для произвольного объема V, то

cru_t = div (k gradu) + F(r,t)                                                           (2)

(c = c(r), r = r(r), k = k(r)).

Для доказательства (2) достаточно предположить противное; т.е. пусть в некоторой точке подинтегральная функция в (1) не равна нулю. Объём V можно выбрать настолько малым, чтобы в пределах его подинтегральная функция в силу непрерывности сохраняла знак. Тогда интеграл будет отличен от нуля, что противоречит (1).

Заметим, что при выводе уравнения (2) мы предположили, что функция u(r,t) имеет непрерывные частные производные. В дальнейшем мы будем предполагать, что рассматриваемые нами функции имеют столько производных или даже непрерывных производных, сколько нужно для законности проводимых выкладок или рассуждений.

Уравнение (2) называют уравнением распространения тепла. При постоянных с, r, k получаем уравнение теплопроводности

u_t = a²Du + f(r,t),                                                                   (3)

где

, .

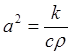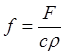Совершенно аналогично выводится уравнение диффузии. Для этого надо воспользоваться законом сохранения вещества и так называемым законом Нернста для плотности потока частиц вещества

j = – D gradu.                                                                        (4)

Здесь и - концентрация частиц диффундирующего вещества (т.е. число их в "штуках" в единице объёма), D - коэффициент диффузии. Кроме того, вместо сr в выражении, аналогичном Q₂, вообще говоря, надо писать коэффициент пористости среды с, в которой происходит диффузия. Уравнение диффузии имеет вид

cu_t = div (D gradи) + F(r,t).                                                           (5)

Замечание. Уравнение (5) можно вывести при некоторых достаточно простых предположениях в диффузионном приближении из кинетического уравнения, широко используемого в физике. Качественное представление о процессах диффузии и теплопроводности можно получить, например, из книги Л.Д.Ландау, А.И.Ахиезер, Е.М.Лифшиц, Курс общей физики, Наука, 1965, гл. XIV.

§3. Уравнения для напряжённостей электрического и магнитного поля в вакууме

Пусть в некоторой среде имеется переменное электромагнитное поле. Введём обозначения: Е(г,t) - напряжённость электрического поля, H(r,t) - напряжённость магнитного поля, e - диэлектрическая постоянная среды, m - коэффициент магнитной проницаемости, r - плотность электрических зарядов, j - плотность тока проводимости.

Поведение электромагнитного поля описывается уравнениями Максвелла, которые в гауссовой системе единиц имеют вид

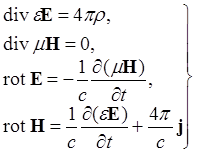                                                            (1)

(с = 3·10¹⁰ см/сек - скорость света).

Уравнения (1) выражают в дифференциальной форме соответственно закон Кулона, замкнутость магнитных силовых линий, закон Фарадея и закон Био-Савара и его обобщение (см. [4]).