Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 11

§1. Классификация линейных относительно старших производных дифференциальных уравнений 2-го порядка

Рассмотрим уравнение

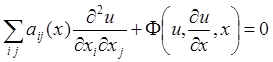                                                     (1)

с непрерывными коэффициентами а_ij(x). Это уравнение очень общее, ничего конкретного о нём неизвестно. Постараемся упростить его с помощью замены независимых переменных

y_l = y_l(x₁,...,x_n) = y_l(x) (l = 1,...,n),                                                  (2)

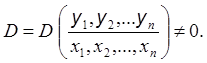
Выясним, прежде всего, по какому закону преобразуются коэффициенты a_ij(x). Так как якобиан D ¹ 0, то в некоторой окрестности точки х = x₀ можно выразить переменные х через переменные y: х = х(y). Обозначим и(х(y)) = ô(y). Имеем:

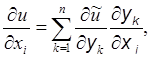                                                                  (3)

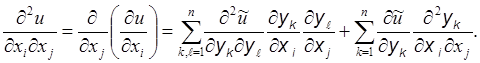                                 (4)

Подставим (3) и (4) в (1):

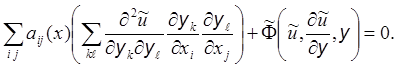
Изменим порядок суммирования:

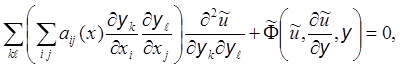
или

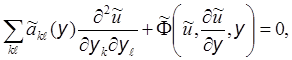                                                   (5)

где

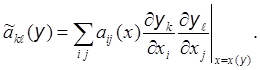                                                       (6)

Фиксируем точку х = x₀. Пусть

y(x₀) = y₀,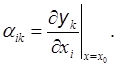 

Тогда

Подберём теперь таким образом числа a_ik, чтобы при "замороженных" коэффициентах a_ij(x₀) уравнение (5) упростилось.

Полученная формула преобразования коэффициентов a_ij в точке х = x₀ совпадает с формулой преобразования коэффициентов квадратичной формы

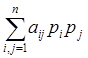                                                                        (7)

при невырожденном линейном преобразовании

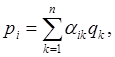                                                                     (8)

где det a_ik ¹ 0. Действительно,

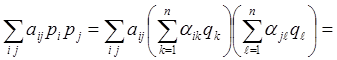
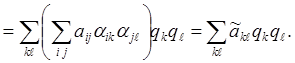
Поэтому, чтобы упростить уравнение (1) с помощью замены переменных (2), достаточно упростить в точке х = x₀ квадратичную форму (7). Как классифицировать квадратичные формы, известно из курса линейной алгебры,^[3] где доказывается, что существует по крайней мере одно невырожденное линейное преобразование (8), при котором квадратичная форма (7) приводится к сумме квадратов и принимает следующий канонический вид:

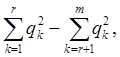
                                                             (9)

При этом в силу закона инерции квадратичных форм целые числа r и т не зависят от преобразования (8), т.е. совокупность знаков в (9) является инвариантом уравнения. Отсюда следует, что главную часть дифференциального уравнения (1) можно привести к виду

 

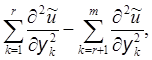
Этот факт позволяет классифицировать дифференциальные уравнения вида (1) в зависимости от значений а_ij(x₀). Если в квадратичной форме (9) т = n и все слагаемые одного знака (т.е. r = т или r = 0), то уравнение (1) называют уравнением эллиптического типа; если т = n, но имеются слагаемые разных знаков (1 ≤ r ≤ n – 1), то уравнение (1) называют уравнением гиперболического типа; если т < п – параболического типа.

Примеры. 1) Уравнения Лапласа и Пуассона - эллиптического типа, волновое уравнение - гиперболического типа, уравнение теплопроводности - параболического типа. Аналогичные выводы можно сделать об уравнениях, описывающих процессы колебаний, распространение тепла и стационарные процессы.

2) Есть уравнения более сложной природы. Например, уравнение Трикоми  при y > 0 - эллиптического типа, при y < 0 - гиперболического, а при y = 0 - параболического типа.

§2. Приведение дифференциальных уравнений 2-го порядка с двумя независимыми переменными к каноническому виду

В §1 для классификации уравнений, линейных относительно старших производных, мы поступали следующим образом: фиксировали точку x, "замораживали" тем самым коэффициенты, затем исследовали соответствующую квадратичную форму.

Рассмотрим подробнее вопрос о том, можно ли привести уравнение к каноническому виду одним и тем же преобразованием в некоторой достаточно малой области, содержащей т. х = x₀. Если a_ij - постоянные коэффициенты, то по известным числам , приводящим квадратичную форму к каноническому виду, можно восстановить . В случае переменных коэффициентов a_ij необходимо, чтобы число условий

ã_kl = 0, l ≠ k, k, l = 1, 2,…, n (ã_kl = ã_lk);

ã_ll = e_lã₁₁, l = 2, 3,…, n; ã₁₁ ≠ 0; e_l = 0, ±1

не превосходило число неизвестных функций y_l(x) (l = 1, 2,…, n):

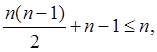 т.е. n ≤ 2.