Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 8

Силы, действующие на каждый элемент объема dV независимо от того, существуют или нет рядом с объемом dV другие части жидкости, - это внешние объемные силы. Если F(r,t) - объемная плотность силы, то сила, приложенная к объему V, выразиться интегралом (векторным) .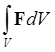

Примеры внешних сил:

а) среда находится в поле силы тяжести: F = rg;

б) частицы жидкости (газа) могут нести электрический заряд и испытывать действие электромагнитного поля:  (ионы в плазме, j - плотность тока , r_е - плотность зарядов).

Кроме объёмных сил существуют силы, обусловленные взаимодействием между различными частицами среды. Если воспользоваться третьим законом Ньютона, то становится ясно, что произойдёт уравновешивание сил взаимодействия между всеми внутренними частицами объёма V и останутся только силы, исходящие от частиц, лежащих снаружи поверхности S и приложенные к "поверхностным" частицам объёма V. Сила, приложенная к элементу поверхности dS, будет равна pdS. Здесь р - вектор поверхностной силы, отнесённый к единице площади. В случае отсутствия сил вязкости вектор р направлен по нормали к поверхности внутрь объёма V и будет обозначать давление. Тогда сила, приложенная ко всей поверхности S будет равна

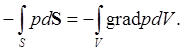                                                               (2)

где

Это равенство следует из теоремы Гаусса-Остроградского

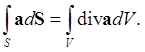
Действительно, пусть а = ef(x,y,z,t), где e - произвольный постоянный вектор. Тогда

div a = e · gradf,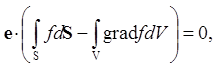 

откуда

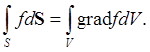
Если пренебречь силами вязкости (будем считать жидкость идеальной), то при отсутствии внешних сил из (2) видно, что на каждый элемент объёма, жидкости dV действует со стороны окружающей его жидкости сила – gradpdV. Так, например, в одномерном случае, действительно, получаем

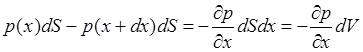
(ось х направлена вдоль оси трубы, S - поперечное сечение).

Согласно второму закону Ньютона для жидкой частицы с массой rdV имеем

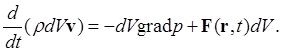
Масса жидкой частицы rdV от времени не зависит. Отсюда получаем уравнение Эйлера:

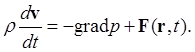                                                             (3)

Производная  по смыслу вывода определяет не изменение скорости жидкости в данной неподвижной точке пространства, а изменение скорости v(r,t) определённой, передвигающейся в пространстве по траектории r = r(t) частицы жидкости. Эту производную можно выразить через величины, относящиеся к неподвижным в пространстве точкам:

v = v(r,t) = v(x,y,z,t), где х = x(t), y = y(t), z = z(t);

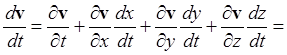
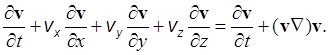
Перепишем (З) в виде

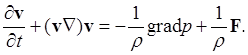                                                        (4)

Замечание, Если рассматривать плазму как проводящую жидкость, то в магнитном поле уравнение Эйлера принимает вид

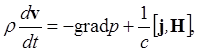
где второе слагаемое справа есть сила Лоренца. Это уравнение широко применяется в магнитной гидродинамике.

3°. Последнее из системы уравнений газодинамики определяет связь р и r для данного процесса: р = р(r). Например, для адиабатического процесса сжатия идеального газа р/р^g = const (g = c_p/c_v, c_p и с_v - удельные теплоёмкости газа при постоянном давлении и объёме); для несжимаемой жидкости r = const.

В общем случае это уравнение выражает закон сохранения энергии. Изменение внутренней энергии вещества происходит за счёт работы сил сжатия, которую производит окружающая среда, а также вследствие выделения энергии от посторонних источников (например, за счёт притока тепла), которые считаются заданными:

de = – pdV + dQ.                                                                     (5)

Если в качестве независимых переменных, задающих условия, в которых находится вещество, выбрать температуру Т и плотность r, то термодинамические функции р и e могут быть выражены через них:

p = р(r,T), e = e(r,Т).                                                             (6)

Здесь р - давление, e - удельная внутренняя энергия, т.е. энергия, приходящаяся на единицу массы газа. Равенства (6) носят название уравнений состояния вещества.