В повседневной физике и технике обычно интересуются изучением следствий основных физических законов в заданных конкретных условиях, расчетами различного рода эффектов. При этом математическое описание многих физических процессов приводит в зависимости от применяемой теоретической модели к дифференциальным и интегральным уравнениям определенного вида, а также к интегро-дифференциальным уравнениям. Возникающие математические задачи (они могут быть из различных областей физики) имеют много общих черт и составляют содержание предмета математической физики в широком смысле этого слова. Например, одними и теми же уравнениями описываются такие процессы как диффузия, теплопроводность, намагничивание ферромагнетиков. Изучение колебаний различной физической природы приводит к волновому уравнению. Как заметил Л. Больцман, единство природы обнаруживается в поразительной аналогичности дифференциальных уравнений, относящихся к разным областям явлений.
Теория математических моделей физических явлений составляет предмет математической физики. Математическая физика занимает, таким образом, промежуточное положение между математикой и теоретической физикой. Точные рамки этой дисциплины ввиду большого разнообразия вопросов, относящихся к уравнениям математической физики, определить довольно трудно. Так как многие задачи математической физики приводят к уравнениям в частных производных второго порядка, то в более узком смысле под математической физикой иногда понимают теорию линейных дифференциальных уравнений в частных производных второго порядка.
С появлением ЭВМ существенно расширился класс математических моделей, допускающих детальный анализ; появилась реальная возможность ставить вычислительные эксперименты. В этом интенсивном взаимодействии теоретической физики и современной математики создаются качественно новые классы моделей современной математической физики.
В предлагаемом курсе лекций рассмотрены наиболее важные методы решения основных задач математической физики:
1) Метод характеристик.
2) Метод Фурье (метод разделения переменных), опирающийся на разложение решений в ряды по собственным функциям.
3) Метод функций Грина, использующий фундаментальные решения.
Глава I
ПРОСТЕЙШИЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К УРАВНЕНИЯМ РАЗЛИЧНЫХ ТИПОВ. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ.
В этой главе будут рассмотрены несколько характерных физических задач, приводящих к основным уравнениям математической физики.
§1. Уравнение малых поперечных колебаний струны
Будем называть струной натянутую гибкую нить. Математическое выражение понятия гибкости заключается в том, что напряжения, возникающие в струне, всегда направлены по касательной к её мгновенному профилю. Это условие выражает отсутствие сопротивления изгибу, или, другими словами, что сопротивлением при изгибании можно пренебречь по сравнению с натяжением.
Направим ось х вдоль струны в положении равновесия и каждую точку струны будем характеризовать значением ее абсциссы х. Описать процесс колебаний струны - значит задать положения точек струны в различные моменты времени, т.е. компоненты вектора смещения {u1(х,t), и2(х,t), и3(х,t)} точки х в момент t.
Рассмотрим наиболее простую задачу о колебаниях струны. Будем предполагать выполненными следующие условия:
1. Смещения струны лежат в одной плоскости.
2. Ограничимся рассмотрением малых колебаний струны, т.е.
будем пренебрегать величинами высшего порядка малости по сравнению с величиной
ux(x,t) º
= tg a,
где a - угол наклона касательной к
профилю струны в точке х (Рис.1). В частности, будем пренебрегать
квадратом ux по сравнению с единицей.
3. Будем считать, что действующие на струну внешние силы направлены перпендикулярно оси х и вектор смещения в любой момент перпендикулярен к оси x, так что процесс колебаний можно описать одной функцией u(x,t) характеризующей вертикальное перемещение струны.
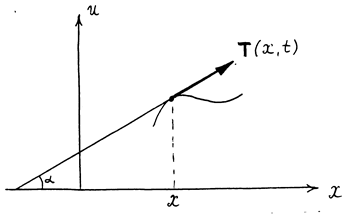
Рис. 1
Малость отклонений приводит к тому, что любой участок струны (х1,х2) не изменяет своей длины. Действительно,
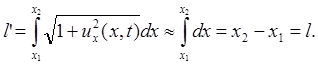
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.