Статика: Расчетные и курсовые работы по дисциплине "Теоретическая механика", страница 8

Системой сочлененных твердых тел называют несколько твердых тел, соединенных между собой посредством шарниров, стержней, нитей или касающихся друг друга. Во многих случаях требуется найти силу, с которой одно сочлененное тело действует на другое. Такая задача обычно решается путем рассмотрения каждого тела системы в отдельности. При рассмотрении отдельного тела остальные тела системы будут являться связями, наложенными на это тело,  и заменяются реакциями связями. При этом необходимо помнить, что силы взаимодействия двух тел для системы являются внутренними, они равны между собой по абсолютной величине, имеют общую линию действия и направлены в разные стороны. Поэтому при рассмотрении равновесия системы всех тел, вместе взятых, внутренние силы не должны входить в уравнения равновесия.

Систему уравнений можно получить, записав уравнения равновесия для системы в целом и для одной части системы в отдельности. Когда же нужно определить силы во внутренних связях, применяют метод, связанный с расчленением системы на части. Для каждой части имеем три независимых условия равновесия (всего их шесть), из совместного решения которых можем найти  шесть неизвестных. 

РАСЧЕТНАЯ РАБОТА №3

Равновесие сочлененных тел

Схемы конструкций плоских систем сочлененных тел представлены на рис.3.5, линейные размеры  и действующие на конструкцию нагрузки - в табл. 3.3.

Определитьсилывзаимодействия, возникающие в промежуточном шарнире B, и усилия вподдерживающихсоставную конструкцию опорах, пренебрегая весами балок.

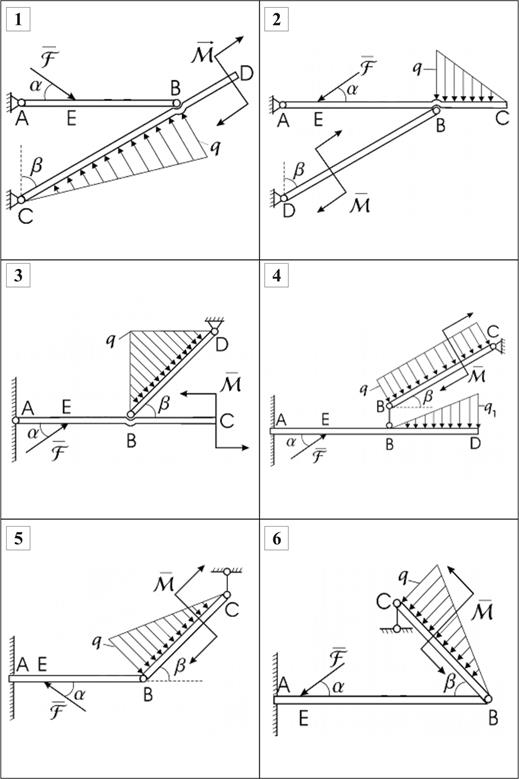
Рис. 3.5. Схемы конструкций сочлененных тел к расчетной работе № 3

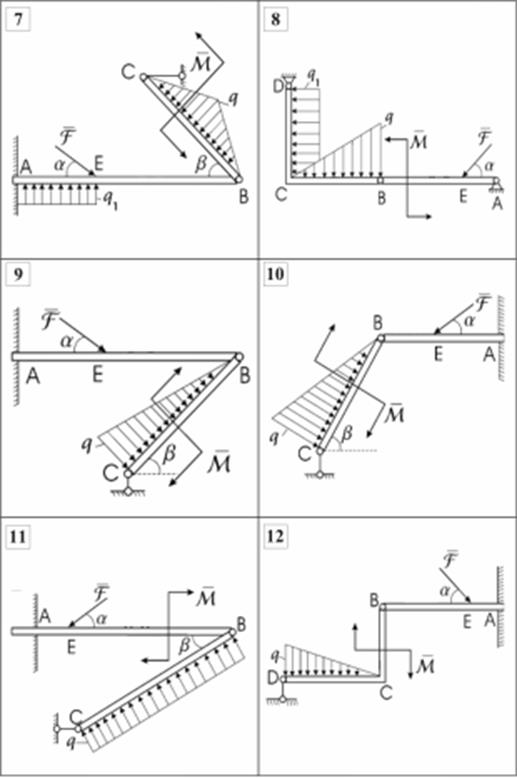
Рис. 3.5 (продолжение)

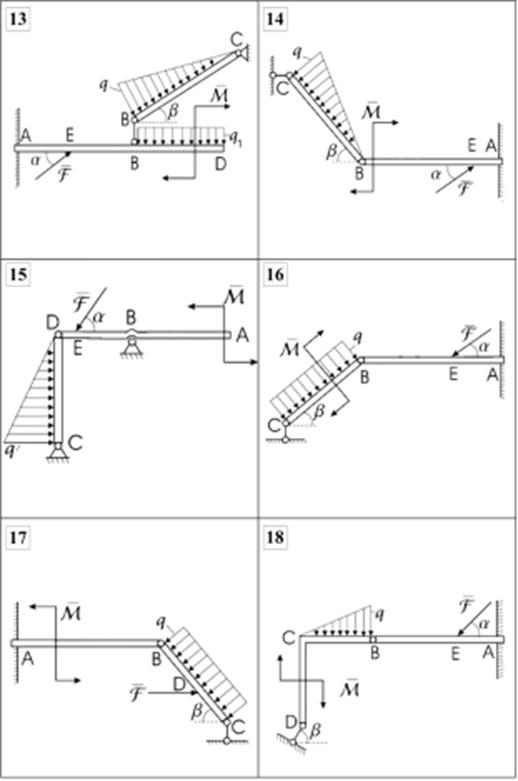
Рис. 3.5 (окончание)

Т а б л и ц а 3.3

                Исходные данные к расчетной работе № 3