Статика: Расчетные и курсовые работы по дисциплине "Теоретическая механика", страница 7

Окончание табл. 3.2

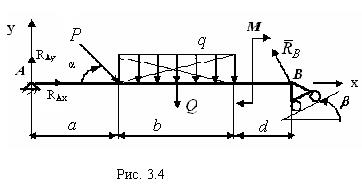
Пример 3.2 выполнения расчетной работы № 2. Равновесие плоской произвольно расположенной  системы сил. Схема балки показана на рис.3.4.

    Дано: Горизонтальная балка АВ  нагружена системой сил: сосредоточенной силой Р = 4 кН, моментом М = 5  кН×м пары сил и равномерно распределенной нагрузкой интенсивности q = 2 кН/ м; размеры а = 2м; b=Зм; d=2 м; углы α =60°; ß =30˚.

Определить: реакции опор    и  , пренебрегая весом балки АВ.

Решение. Рассмотрим равновесие балки АВ под действием заданных активных сил. Для составления уравнений равновесия необходимо равномерно распределенную по закону прямоугольника нагрузку на заданном участке балки b заменить равнодействующей, равной численно площади заштрихованной фигуры-прямоугольника Q=q·b=2·3=6 кН, и приложенной в центре тяжести этой фигуры.

Освобождаем систему от связей, направив реакцию  в катковой опоре (подвижном шарнире В) перпендикулярно плоскости опоры, а реакцию в неподвижном шарнире  А заменяем двумя составляющими - .

Поставленную задачу можно записать коротко следующим образом:

AB , .

Так как число неизвестных реакций (,,) равно трем, то рассматриваемая задача является статически определимой.

Составим уравнения равновесия плоской системы сил, приложенной к балке  АВ:

1.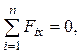 P×cos a-× sin b + = 0;               ;

2.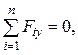 - P×sin a-Q + + × cos b = 0;      ;       

3.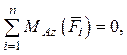 -P× a× sin a - Q×  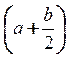- M + ×× cos b = 0.

Из (3):

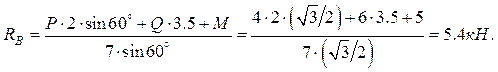
Из (1):  = - P×cos a+ × sin b = - 4 × 0,5+5,4 × 0,5 = 0,7 kH.

Bp (2):  = P×sin a+ Q -× cos b = 4×  + 6 - 5.4   = 4,8 kH.

Для проверки полученных значений опорных реакций можно составить дополнительное уравнение равновесия:

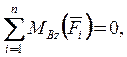       -×7 + P×5×sin a + Q ×3,5 - M = 0;

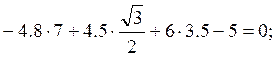    0=0,    значит, реакции определены верно.

Ответ:    = 0.7 кН; = 4.8 кН;    =5.4 кН.

3.2.Равновесие связанных (сочлененных) тел