Статика: Расчетные и курсовые работы по дисциплине "Теоретическая механика", страница 11

Таким образом, для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы компонентов приложенных сил относительно осей декартовых координат были равны нулю и чтобы суммы моментов приложенных сил относительно каждой из осей координат были также равны нулю.

РАСЧЕТНАЯ РАБОТА №4

Равновесие пространственной системы сил

Определить реакции в точках закрепления твердого тела. Схемы конструкций представлены на рис.4.1, исходные данные - в табл. 4.1-4.4. Конкретно задача сформулирована в соответствии с номером рисунка схемы.

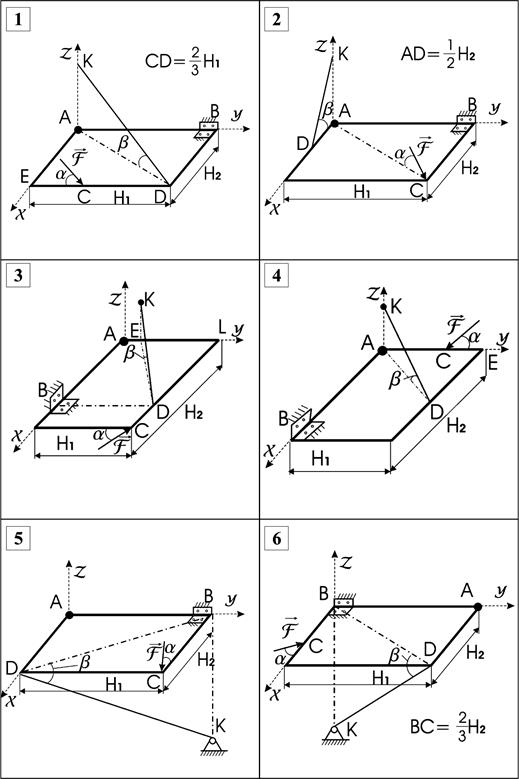
Рис. 4.1. Схемы конструкций к расчетной работе № 4.

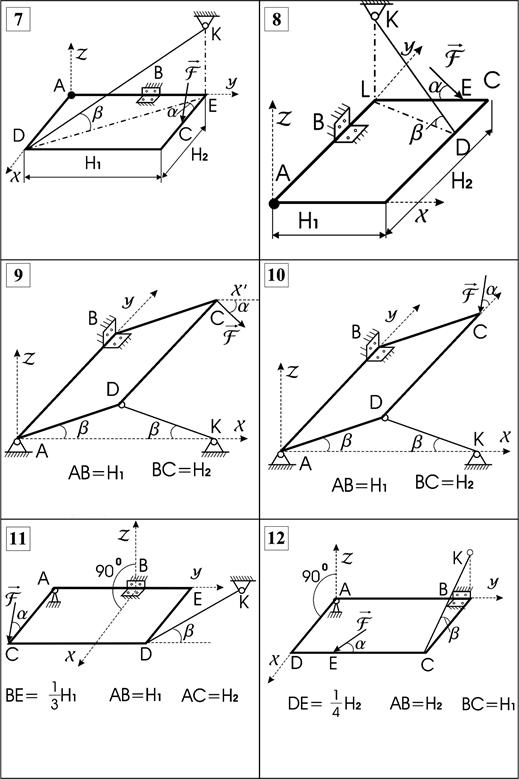
Рис. 4.1 (продолжение)

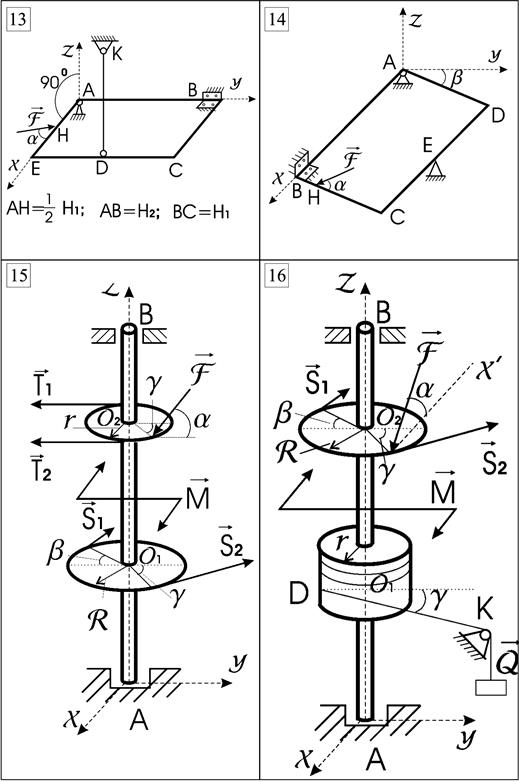
Рис. 4.1 (продолжение)

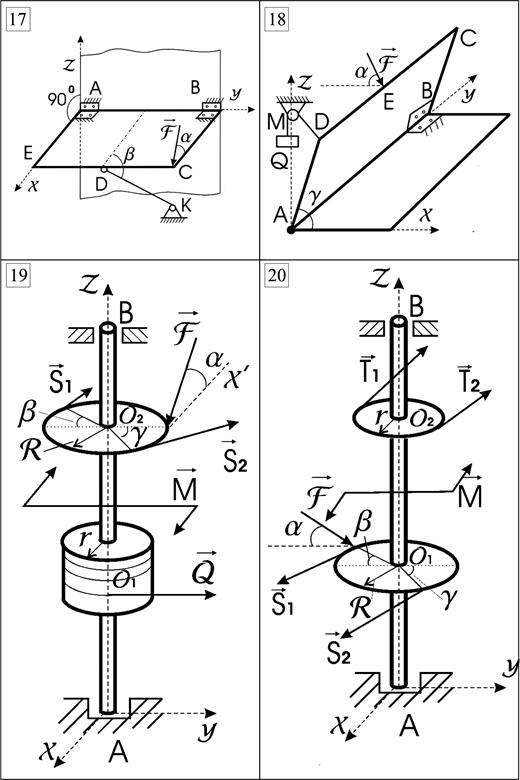
Рис. 4.1 (продолжение)

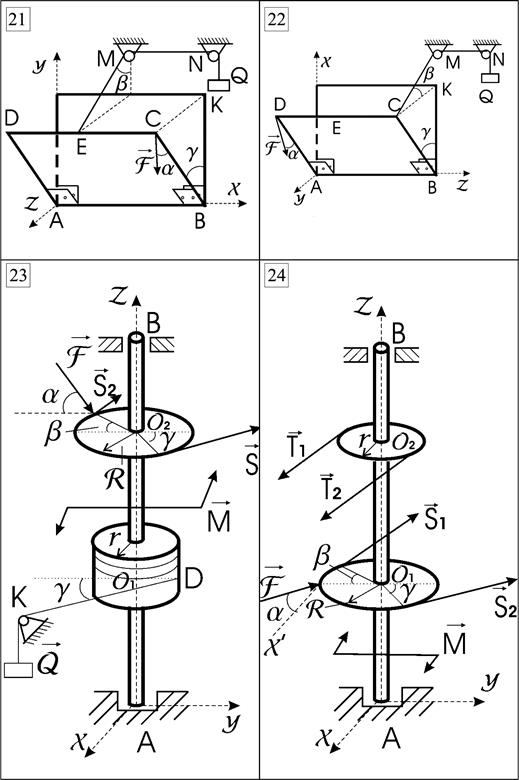
Рис. 4.1 (продолжение)

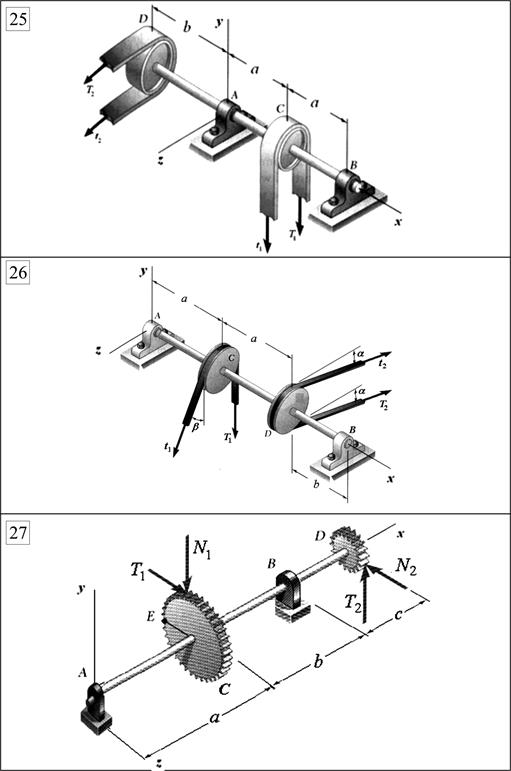
Рис. 4.1 (окончание)

Варианты 1-8:Однородная прямоугольная плита ABCD веса G закреплена в точке A сферическим, а в точке B цилиндрическим шарниром  и поддерживается в горизонтальном положении тросом KD или невесомым стержнем KD (вар.5, 6) , расположенным в вертикальной плоскости и образующим с горизонтальной плоскостью плиты угол b. На плиту действует сосредоточенная нагрузка , образующая угол a с плоскостью плиты. Определить реакции шарниров A и B и натяжение троса  или усилие  в невесомом стержне KD (вар.5, 6). Необходимые линейные размеры, углы, величины сил приведены в табл. 4.1.

Варианты 9-14,17: Однородная прямоугольная плита ABCD веса G закреплена в точке A и B цилиндрическим шарниром и поддерживается в горизонтальном положении тросом КС  (вар. 12)  и  KD  (вар. 13) или невесомым стержнем KD  (вар.9-11, 17), расположенным в вертикальной плоскости и образующим с горизонтальной плоскостью плиты угол b.  В вар. 14  плита опирается на острие в точке E.  На плиту действует сосредоточенная нагрузка , образующая угол a с плоскостью плиты. Определить реакции шарниров A и B и натяжение троса  или усилие в невесомом стержне. Необходимые линейные размеры, углы, величины сил приведены в табл. 4.1.

Т а б л и ц а 4.1

Исходные данные к расчетной работе № 4