Статика: Расчетные и курсовые работы по дисциплине "Теоретическая механика", страница 20

Вариант 11. Определить а) координату  центра тяжести  полого цилиндра с радиусами   и высотой  , т.е. для дискретных значений  , приведенных в табл. 5.7 и  b) ¾ соотношения   для дискретных значений   ,  которые приведены в табл. 5.3 как функции от R, т.е. как  .

          Вариант 12. Определить координату   центра тяжести однородного тела, значения  основных размеров которого приведены в табл.5.3. При выполнении данного варианта расчетной работы можно воспользоваться примером 5.7.

Вариант 13. Определить а) координату  центра тяжести тела для дискретных значений , приведенных в табл. 5.3, т.е.  и  b) ¾ соотношения   для дискретных значения , которые приведены втабл.5.3 как функции  , т.е. .

          Варианты 14, 15, 20. Определить координаты  центра тяжести тел при заданных их размерах.

Вариант 16, 17, 18.  Определить координаты , центра тяжести однородных тел при заданных их размерах.

Вариант 19. Садовый постамент состоит из пирамиды, установленной на  плите высотой  м.  Определить а) центр тяжести постамента от его верхней плоскости,  b) ¾ минимальную высоту плиты , при которой центр тяжести постамента не будет превышать 0.3 м  от его верхней плоскости.

Вариант 21. Определить координаты  и  центра тяжести садовой скамейки, состоящей из двух бетонных (плотностью 2320 ^кг/м³) опор, на которых закреплены сидение и спинка из деревянных досок, плотностью 470 ^кг/м³

и размерами каждой доски:  толщина -b, ширина - d, длина  L=1.18 м.

Пример 5.7 выполнения расчетной работы № 5. Определение положения центра тяжести половины сплошного кругового конуса, представленного  на рис.5.13.

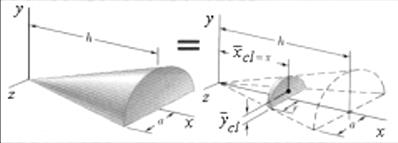
Рис. 5.13

Так как плоскость xy -плоскость симметрии, то центр тяжести лежит в этой плоскости, а координата  0. Толщина выделенного элемента dx, объем которого определяется как    

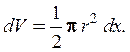
Координаты центра тяжести  и  выделенного элемента определяются как

,    =  , где  определяется из табл. 5.1 для полукруга.

Из рис. 5.13 видно, что 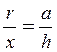, откуда находим 

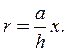
Объем половины сплошного кругового конуса находим как

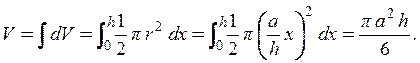
Момент выделенного дифференциального элемента относительно плоскости yz есть  ;  Полный момент рассматриваемоготела относительно  этой же плоскости

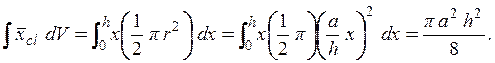
Таким образом, абсцисса центра тяжести тела определяется по формуле

                         ◄

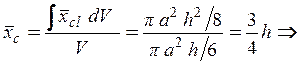
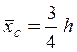Аналогично находим полный момент рассматриваемого телаотносительно  плоскости  xz                                                               

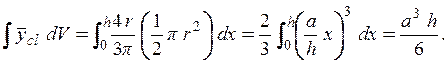
Ордината центра тяжести тела

            ◄

 6. КОМПЬЮТЕРНЫЕ ВАРИАНТЫ ЗАДАЧ

     ПО ОСНОВНЫМ РАЗДЕЛАМ СТАТИКИ

          Рассмотрим компьютерные варианты задач по основным разделам статики, представленные на рис. 6.1, для решения которых и анализа  результатов  требуется программное обеспечение. Линейные размеры и действующие на конструкцию нагрузки приведены  в таблице 6.1. Физико-математические модели соответствуют номеру рисунка схемы.

                    Вариант 1. Положение стержня AB , весом  , один конец  которого закреплен в неподвижном шарнире A , другой конец опирается на шарнир  тележки D , изменяется при медленном перемещении тележки D влевопод действием силы P. Пренебрегая трением, используя компьютерное программное обеспечение, вычислить и построить график изменения величины силы P как функции, т.е.   при изменении  в пределах   . Определить максимальное значение силы  и соответствующее ему значение . 

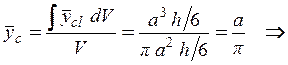
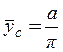Вариант 2. Положение  L - образного рычага определяется  канатом  BE, закрепленным  в точке B. Зная, что на стержень действует сила  , используя компьютерное программное обеспечение, вычислить и графически отобразить   как функции  угла   поворота стержня  при изменении его в следующих пределах  . Определить максимальное значение силы  и соответствующее ему значение.

Вариант 3. Тонкий стержень AB , весом  G  и длиной , шарнирно связан с  ползунами  A и B, свободно перемещающихся соответственно в вертикальной и горизонтальной направляющих. Жесткость пружины , пружина не  напряжена при горизонтальном положении стержня AB. Пренебрегая весом ползунов, вывести уравнения движения стержня в зависимости от  и , которые должны удовлетворять условиям равновесия стержня.  Для заданных величин   a) вычислить и построить график изменения величины жесткости   пружины  как функции  угла поворота  стержня AB, т.е. , при изменении  в следующих пределах:   b) определить два значения угла , соответствующих равновесию стержня при жесткости пружины