Статика: Расчетные и курсовые работы по дисциплине "Теоретическая механика", страница 3

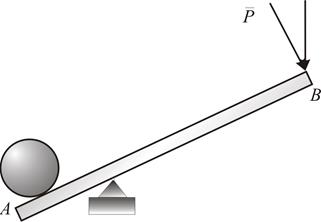
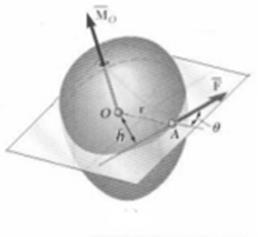
Если рассмотреть подъем груза с помощью рычага АВ (рис.2.1), то из повседневного опыта видно, что одна и та же сила  будет более эффективна (в состоянии поднять больший груз), если она будет приложена под прямым углом к рычагу. Рассмотрим момент силы, приложенной к  твердому телу в точке А, относительно закрепленной точки О тела, вокруг которой тело может вращаться (рис. 2.2). Точка Оназывается центром момента, а кратчайшее

Рис. 2.1                           расстояние h от центра момента до линии действия силы – плечом силы. Вращение тела зависит в конечном итоге от величины

F h и ориентации треугольника  ОАF , и поэтому момент силы удобнее рассматривать как вектор.

Пусть - радиус-вектор, проведенный из точки О в точку А приложения силы  к телу (рис.2.2).

Тогда моментом силы  относительно центра О называется вектор ₀ (), приложенный в центре О перпендикулярно плоскости, проходящей через векторы  и в ту сторону, откуда поворот от вектора  к вектору  кажется происходящим против хода часовой стрелки, и равный

Рис.2.2                      ₀() = ´.

Модуль векторного произведения  ç₀()ç = F r sinq = F h,  где  q  - угол между векторами  и.

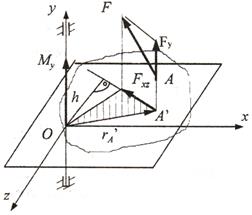
Момент силы относительно оси

Рассмотрим тело, которое может вращаться вокруг неподвижной оси у, и к нему в точке А  приложена сила   (рис.2.3). Через произвольную точку оси проведем плоскость, перпендикулярную оси, а саму ось возьмем за одну из осей декартовой системы координат с началом в точке О. Разложим силу  

Рис.2.3                                     на две составляющие: , параллельную оси Oy, и, равную проекции силы  на плоскость xОz. Составляющая  не может повернуть тело вокруг оси Oy , а может лишь сдвигать его вдоль оси. Следовательно, вращающийэффект силы  будет создаваться только ее проекцией на плоскость, перпендикулярную оси Oy, т.е. моментом проекции этой силы. Моментом силыотносительно произвольной оси Oy называется момент проекции силы на плоскость , перпендикулярную оси Oy, взятый относительно точки пересечения плоскости с осью.

Обозначим момент силы относительно оси Оy - , радиус-вектор проекции точки  А  на плоскость - . Тогда

 = , а его величина   

Момент силы относительно оси считается положительным, если с положительного направления оси Oy, поворот тела, вызываемый моментом, представляется происходящим против хода часовой стрелки.

Из полученной формулы следует, что момент силы относительно оси равен нулю в двух случаях: если сила параллельна оси, т.е. когда проекция силы на плоскость равна нулю, и когда плечо силы h равна нулю, т.е. когда линия действия силы пересекает ось. В обоих этих случаях сила и ось лежат в одной плоскости.

3. РАВНОВЕСИЕ ПЛОСКОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ

Механический смысл равновесия произвольной системы сил, приложенной к твердому телу, состоит в том, что необходимым и достаточным условием равновесия является равенство нулю главного вектора  этих сил и главного момента  сил относительно произвольно выбранного центра.

В аналитической форме  условия равновесия сводятся к следующим:

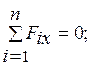
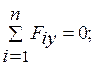
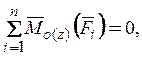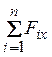1)        где  и 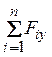- сумма проекций всех сил (активных и реакций связей) на оси x и y, 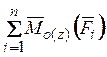 - сумма моментов всех сил относительно центра , ¾ первая форма условий равновесия плоской  произвольной системы сил;

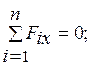
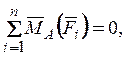
2)   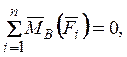  прямая АВ не должна быть перпендикулярна оси x, ¾вторая форма условий равновесия;

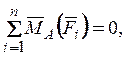
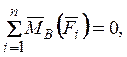
3)   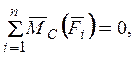точки  А, В, С не лежат на одной прямой, ¾ третья форма условий равновесия.

Систему координат, с целью упрощения решения задачи, следует выбирать так, чтобы хотя бы одна из осей была перпендикулярна к какой-нибудь неизвестной силе, а за центр моментов - точку, которая лежит на линии действия по крайней мере одной неизвестной силы. При решении задачи по третьей форме уравнений равновесия (три суммы моментов) за центр моментов нужно брать точки пересечения линий действия неизвестных сил, если эти силы рассматривать попарно.