расстояние относительно опоры K,
на котором должен располагаться противовес для обеспечения максимальной
грузоподъемности крана, равно ![]() .
.
Решение. Рассмотрим равновесие крана
(рис.3.2). К нему приложены активные заданные силы: вес крана ![]() , вес груза
, вес груза ![]() и вес
противовеса
и вес
противовеса ![]() . На кран наложены
. На кран наложены 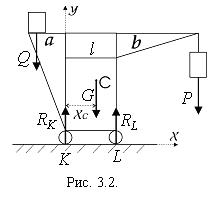 две связи - катковые опоры K,
L, которые не допускают смещения крана вниз от
опорной поверхности по вертикали, но не препятствуют его повороту вокруг точекK, L. Так как
трением в опорах пренебрегаем, то реакции опор будут направлены нормально к поверхности.
две связи - катковые опоры K,
L, которые не допускают смещения крана вниз от
опорной поверхности по вертикали, но не препятствуют его повороту вокруг точекK, L. Так как
трением в опорах пренебрегаем, то реакции опор будут направлены нормально к поверхности.
Теперь рассматриваем равновесие крана как свободного тела,
находящегося под действием сил ![]() ,
,![]() .
.
Опрокидывание ненагруженного крана под действием противовеса возможно вокруг левой опоры K в направлении против часовой стрелки, при этом кран правой опорой L только касается поверхности, не оказывая на нее никакого давления. Поэтому вес противовеса находится из условия равенства моментов опрокидывания и устойчивости
![]() ,
откуда
,
откуда 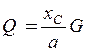 =
= 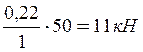 .
.
Максимально загруженный кран может опрокидываться вокруг правой опоры L по часовой стрелке. Поэтому уравнение моментов составим относительно точки L.
![]()
Из полученного уравнения находим наибольший вес поднимаемого груза
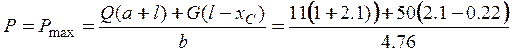 =27 кН.
=27 кН.
Для определения реакций в опорах крана составим уравнения равновесия для полученной системы сил по третьей форме ¾ два уравнения моментов относительно опор K иL:
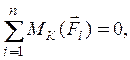
![]()
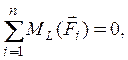
![]()
Из полученных уравнений находим искомые реакции ![]()
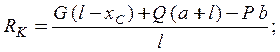
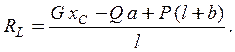
РАСЧЕТНАЯ РАБОТА №2
Равновесие плоской произвольно расположенной системы сил
Определить реакции связей.
Схемы конструкций представлены на рис.3.3,
исходные данные – в табл.3.2, где G - сила тяжести, P - активная сила, ![]() - равномерно
распределенные нагрузки, M - момент.
- равномерно
распределенные нагрузки, M - момент.
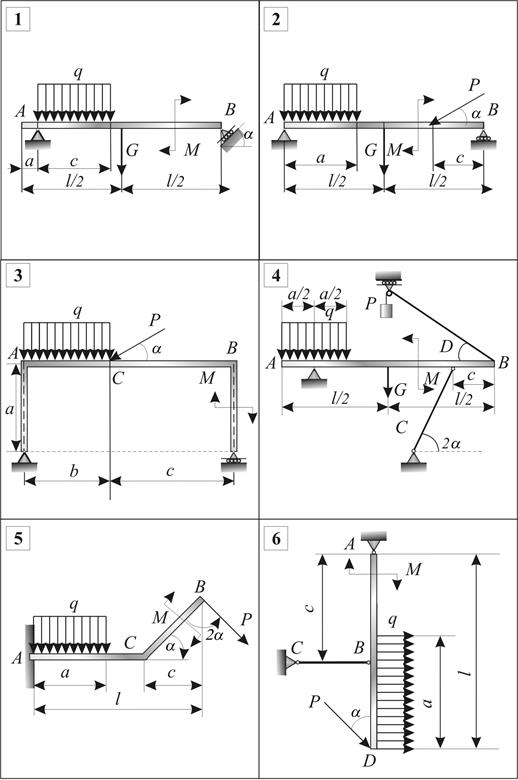
Рис. 3.3. Схемы конструкций к расчетной работе № 2
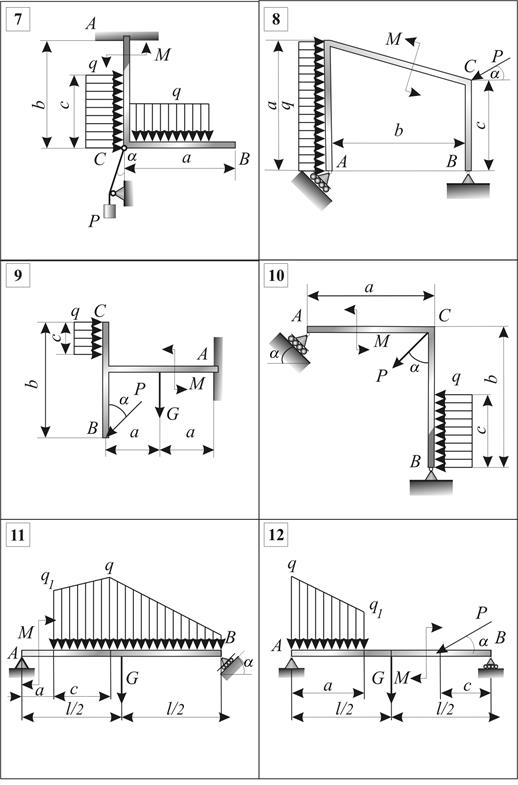
Рис. 3.3 (продолжение)
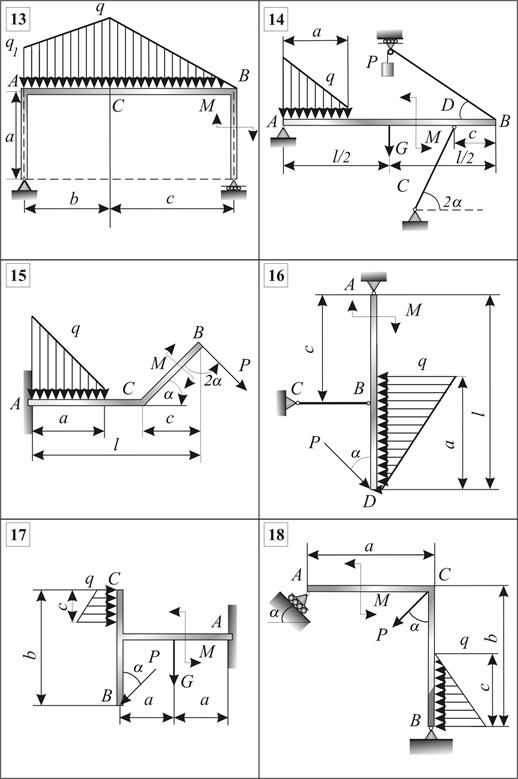
Рис. 3.3 (окончание)
Т а б л и ц а 3.2
Исходные данные к расчетной работе № 2
|
№ схе- мы |
Линейные размеры, м |
Угол, ° град |
G |
P |
|
M |
|||
|
a |
b=l |
c |
a |
кН |
кН/м |
кН×м |
|||
|
1 |
2 3 3 |
4 6 6 |
1 2 3 |
45 90 30 |
6 8 4 |
- |
3 4 5 |
7 8 9 |
|
|
2 |
2 3 3 |
4 6 6 |
1 2 3 |
30 45 60 |
6 8 4 |
5 6 8 |
2 3 4 |
9 8 7 |
|
|
3 |
2 2 2 |
4 4 3 |
1 0 1 |
30 60 90 |
- |
2 3 4 |
4 5 6 |
9 8 6 |
|
|
4 |
1 2 2 |
4 5 5 |
1 1 2 |
30 45 60 |
6 7 8 |
5 4 6 |
2 4 6 |
8 9 6 |
|
|
5 |
2 5 3 |
4 10 8 |
2 4 2 |
30 45 60 |
- |
4 5 6 |
3 4 6 |
6 7 9 |
|
|
6 |
3 2 2 |
4 2 3 |
3 1 1 |
30 60 45 |
- |
6 7 8 |
2 4 6 |
8 9 6 |
|
|
7 |
2 2 3 |
5 6 8 |
2 3 3 |
60 30 45 |
- |
9 8 7 |
2 4 6 |
5 6 8 |
|
|
8 |
2 4 2 |
3 5 2 |
1 2 2 |
45 60 30 |
- |
3 4 5 |
2 4 6 |
5 8 9 |
|
|
9 |
2 2 2 |
4 2 6 |
1 2 4 |
30 60 45 |
4 6 8 |
5 6 8 |
4 6 8 |
8 9 7 |
|
|
10 |
4 4 3 |
4 3 4 |
2 3 3 |
30 45 60 |
- |
7 8 9 |
1 2 4 |
8 9 7 |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.