Определитьреакции шарниров и натяжение троса.
Р е ш е н и е.Освобождаем плиту от
связей и рассматриваем ее равновесие под действием заданнойсилы веса G, сосредоточенной силы![]() , реакций
в шарнирах
, реакций
в шарнирах ![]() ,
, ![]() и
натяжения троса
и
натяжения троса ![]() .
.
Поставленную задачу можно записать коротко следующим образом:
ABCD![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
Задача статически определима, т.к. число неизвестных (![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() )
соответствует числу уравнений равновесия для пространственной системы сил,
приложенных к плите. Силу натяжения
)
соответствует числу уравнений равновесия для пространственной системы сил,
приложенных к плите. Силу натяжения ![]() необходимо геометрически
разложить на три составляющие:
необходимо геометрически
разложить на три составляющие: ![]() ,
, ![]() ,
, ![]() и вычислить
(см. рис. 4.3)
и вычислить
(см. рис. 4.3)
![]() =
= ![]()
![]() =
= ![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
1.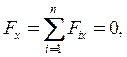
![]() +
+ ![]() = 0;
= 0;![]()
![]() = -
= -![]() +
+![]() =1.45 кН;
=1.45 кН;
2.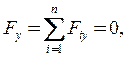
![]() +
+![]() -
-![]() = 0;
= 0;![]()
![]() = -
= -![]() +
+![]() =
=
= 2.77 кН;
3.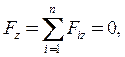 -G -
-G -![]() +
+![]() +
+ ![]() +
+![]() = 0;
= 0;![]()
![]() = G +
= G +![]() -
-![]() -
-![]() =
=
= 0.67 -1.33 кН;
4.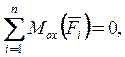 - G×
- G× ![]() +
+![]()
![]() +
+ ![]() a +
a + ![]() sina ×а = 0;
sina ×а = 0; ![]()
![]() =
=![]() =
=
= -1.33 кН;
5.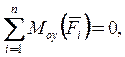 G×
G×![]() +
+![]() ×b -
×b - ![]() sina ×b = 0;
sina ×b = 0; ![]()
![]() =
=![]() =6 кН;
=6 кН;
6. 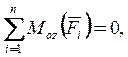
![]() ×b -
×b -![]() ×a + = 0;
×a + = 0; ![]()
![]() =
= ![]()
![]() = 1.15 кН.
= 1.15 кН.
Уравнения равновесия для пространственной системы сил, приложенных к телу, удобно представлять в табличном виде:
|
|
|
|
|
|
|
|
|
1 |
|
0 |
-
|
0 |
-
|
0 |
|
2 |
|
0 |
|
-
|
|
|
|
3 |
|
|
|
|
0 |
0 |
0 |
4 |
|
|
0 |
|
|
0 |
-
|
5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
ß |
ß |
ß |
ß |
ß |
ß |
||
|
|
|
|
|
|
|
 Решая полученную систему
уравнений, определяем искомые реакции. По заданным компонентам определяются
реакции
Решая полученную систему
уравнений, определяем искомые реакции. По заданным компонентам определяются
реакции ![]() ,
, ![]() . Направления
реакций, имеющих по результатам расчета знак “ минус”, противоположны тем, которые
указаны на схеме сил, но изменять ничего не надо.
. Направления
реакций, имеющих по результатам расчета знак “ минус”, противоположны тем, которые
указаны на схеме сил, но изменять ничего не надо.
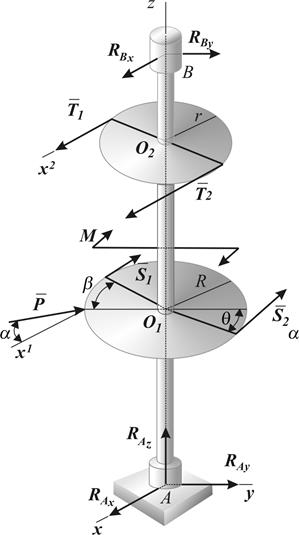
Пример 4.3 выполнения расчетной работы № 4. Равновесие пространственной произвольной системы сил, приложенной к одному телу (рис.4.4).
Дано:Вертикальный ворот закреплен в точке А подпятником, а в точке В – цилиндрическим шарниром и нагружен так, как это показано на рис. 4.4.
Определить при равновесии силы реакций закрепленных точек, а также натяжение S1 ведущей цепи 1, если S1= а×S2, где S2 – натяжение ведомой цепи 2 . Заданы: AO1 = O1O2 = (1/a) AB; AB =1.2 м; r = (b/a)R; R=
= 0.6 м; P =100 H; T1 =100 H; M = 10a Hм; a = 4,
b= 2 - безразмерные коэффициенты; углы
a=60°,b= 30°,q =
30° , образованные радиусами, проведенными в точке схода цепи (точке
касания), с диаметром колеса, парал Рис.4.4 лельным оси Ay. Поставленную задачу можно записать коротко следующим образом:AB![]()
![]()
Решение примера 4.3 (рис.4.4) приведено в виде таблицы:
№ |
|
|
|
|
|
|
|
1 |
|
-
|
0 |
-
|
|
|
|
2 |
|
0 |
0 |
0 |
0 |
0 |
M |
3 |
|
|
0 |
0 |
0 |
|
|
4 |
|
|
0 |
0 |
0 |
|
|
5 |
|
-
|
|
0 |
|
|
-
|
6 |
|
-
|
|
0 |
|
|
|
7 |
|
|
|
|
0 |
0 |
0 |
8 |
|
|
|
0 |
-
|
|
0 |
|
|
|
|
|
|
|
||
ß |
ß |
ß |
ß |
ß |
ß |
||
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.