Статика: Расчетные и курсовые работы по дисциплине "Теоретическая механика", страница 17

Рис.5.4

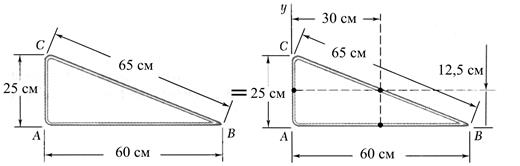
Пример 5.2.  Определение центра тяжести однородного стержня (провода) (рис.5.5)

	Элементы отрезков
1	AB	60	30	0	18×102	0
2	BC	65	30	125	19.5×102	8.13×102
3	CA	25	0	125	0	3.13×102
	Итого	=150			=37.5×102	=11.26×102

   ◄

 ◄

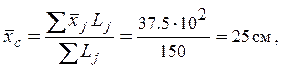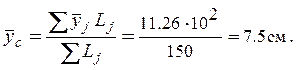Рис.5.5

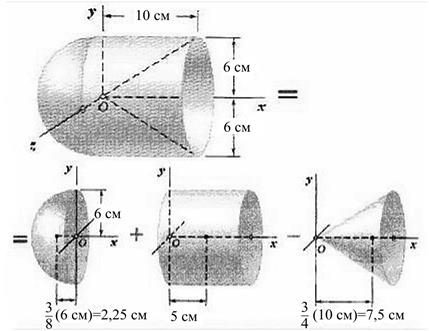
Пример 5.3. Определение центра тяжести однородного объемного тела (рис 5.6)

 

	Элементы объемного     тела	Объем,
1	полусфера		-2.25	-10.16×102
2	цилиндр		+5	+56.55×102
3	конус		+7.5	- 28.28×102
	Итого	12.06×102		=18.09×102

     ◄

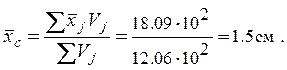Рис. 5.6

Метод симметрии. Центр тяжести симметричных тел. Если однородное тело имеет плоскость, ось или центр материальной симметрии, то его центр тяжести  находится соответственно в плоскости, на оси или в центре симметрии. Например, центр тяжести дуги окружности (рис. 5.7) или однородного тела вращения (рис.5.10, 5.11) лежат на оси симметрии,  шара - в его центре  и т.п.

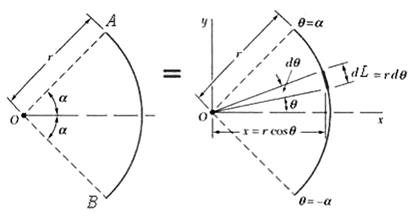
Пример 5.4. Центр тяжести дуги окружности (рис.5.7) радиусом r  c центральным углом  2a. Центр тяжести лежит на оси симметрии Ox. Для определения абсциссы  выделим элемент дуги длиной . Длина дуги окружности                                 определяется как

Рис. 5.7                                 

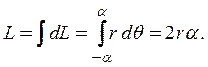 Так как 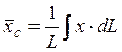 , где  = ,

     ◄

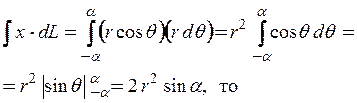
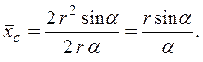Для дуги полуокружности  имеем  Так как < a, то

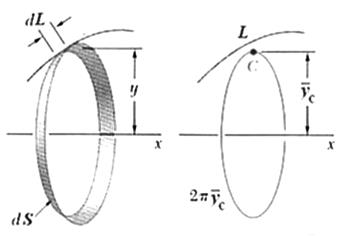центр тяжести лежит внутри сектора АОВ (рис.5.7).

Рис. 5.8                     

Теоремы Паппа - Гюльдена, позволяют определить положение центра тяжести линии  и плоской фигуры в тех случаях, когда известны поверхность или объем тела, образованных вращением линии или фигуры вокруг оси, лежащей в их плоскости.

Теорема 1. Площадь поверхности, образованной вращением плоской   кривой вокруг оси, лежащей в плоскости кривой и ее не пересекающей, равна произведению длины этой линии на длину окружности, описываемой ее центром тяжести (рис. 5.8 и рис. 5.10).

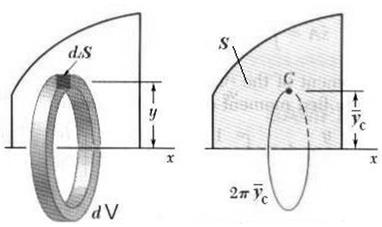Теорема 2. Объем тела, образованного вращением плоской фигуры вокруг оси, расположенной в плоскости фигуры и ее не пересекающей, равен произведению площади фигуры на длину окружности, описываемой ее центром тяжести (рис.5.9).

                                      

Рис.5.9                                                                             

Пример 5.5. Определение положения центра тяжести линии в том случае, когда известна поверхность, образованная вращением линии или фигуры вокруг оси, лежащей в их плоскости (рис. 5.10).

Согласно теоремы 1 Паппа - Гюльдена , с учетом величины абсциссы четверти окружности взятой из табл. 5.1, и равной  ,  находим абсциссу центра тяжести этой линии относительно вертикальной оси вращения  длину четверти окружности   и

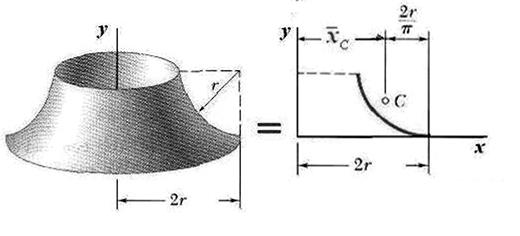
Рис. 5.10

площадь поверхности  ее вращения, вокруг вертикальной оси y:

     ◄

Метод интегрирования. Когда тело нельзя разбить на составные части, центр тяжести которых известен, используют метод интегрирования, являющийся универсальным.

Пример 5.6. Определить центр тяжести полуэллипсоида вращения (рис.5.11).