Статика: Расчетные и курсовые работы по дисциплине "Теоретическая механика", страница 4

Задание на равновесие плоской системы сил состоит из трех расчетных работ: двух №1 и №2 ¾ на равновесие одного тела под действием плоской произвольной системы сил; и  №3 ¾ на равновесие системы сочлененных тел.

3.1. Равновесие одного тела

Задача на равновесие одного тела под действием плоской произвольной системы сил решается в следующей последовательности:

- выделить тело, равновесие которого рассматривается;

- указать заданные активные силы, приложенные к телу;

- в случае несвободного тела мысленно освобождаем тело от связей,  заменив их действием реакций связей (направление которых выбирается исходя из вида связи (табл.2.1);

- составить расчетную схему, указав на ней (на рисунке схемы конструкции) все приложенные к телу активные силы, моменты и реакции связей, распределенные нагрузки замещаются при этом сосредоточенными силами с указанием точек их приложения;

- определить число неизвестных реакций и число возможных уравнений равновесия и установить, является ли рассматриваемая задача статически определимой;

- выбрать систему координат и составить уравнения равновесия;

- решить систему уравнений и определить все неизвестные величины;

- провести качественный анализ полученного решения и его соответствия механическим условиям задачи.

Задачу на равновесие плоской системы сил, приложенной к одному телу, рассматриваем для двух случаев:

Расчетная работа №1. Равновесие тела, которое может опрокидываться;

Расчетная работа №2. Равновесие плоской произвольно расположенной системы сил.

РАСЧЕТНАЯ РАБОТА №1

Равновесие тела, которое может опрокидываться

При выполнении расчетной работы №1 на опрокидывание рассматривается предельное положение, когда тело находится в состоянии неустойчивого равновесия и может перейти из состояния покоя в движение. Всякое даже незначительное изменение элементов конструкции или сил, действующих на тело, ведет к опрокидыванию (вращению) конструкции вокруг некоторой оси, называемой осью опрокидывания. Некоторые активные силы, приложенные к телу, образуют пары, которые стремятся опрокинуть тело. Сумма моментов таких сил относительно оси опрокидывания называется моментом опрокидывания; другая часть активных сил создает пары, которые стремятся возвратить тело в исходное положение. Сумма моментов этих сил относительно оси опрокидывания называется моментом устойчивости.

Определить:* вес противовеса , при котором не произойдет опрокидывание ненагруженного крана;*максимальный вес  груза, который сможет поднять кран; *реакции в опорах крана  при максимальной нагрузке.

Схемы конструкций механических кранов представлены на рис.3.1, а

исходные данные: веса  кранов, положение центра тяжести C и линейные размеры  - в табл 3.1.

Элементы конструкции принимаются абсолютно жесткими, стержневые детали - сплошными и невесомыми, трение в шарнирах и опорах отсутствует.  

Пример 3.1 выполнения расчетной работы №1. Равновесие плоской произвольной системы сил, приложенной к одному телу, которое может опрокидываться.

Дано: Механический кран (рис.3.2) веса  установлен на горизонтальной поверхности. Расстояние между опорами , абсцисса центра тяжести крана , вылет стрелы крана относительно опоры ,

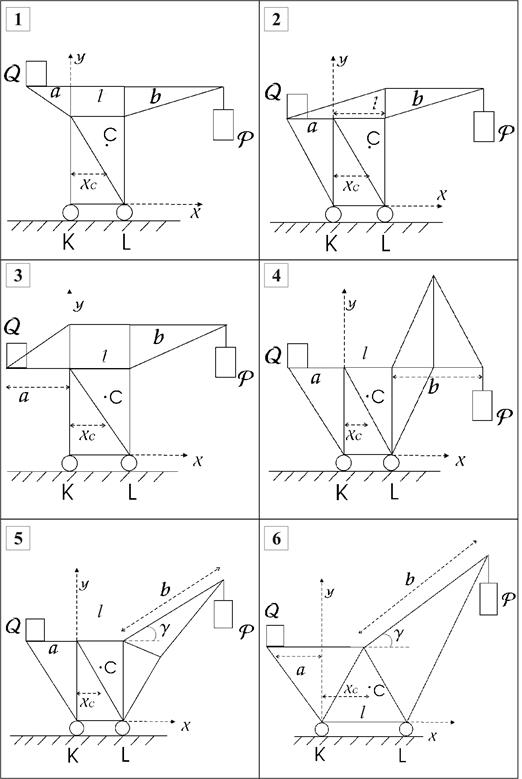
Рис. 3.1. Схемы конструкций механических кранов к расчетной работе № 1

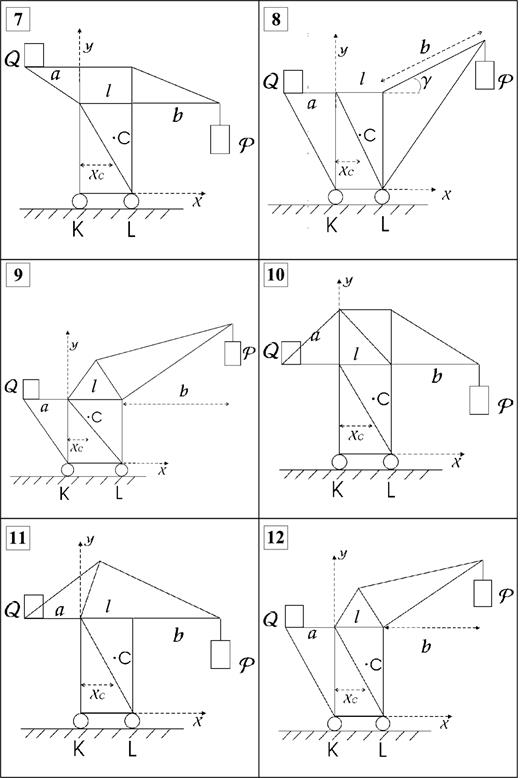
Рис. 3.1 (продолжение)

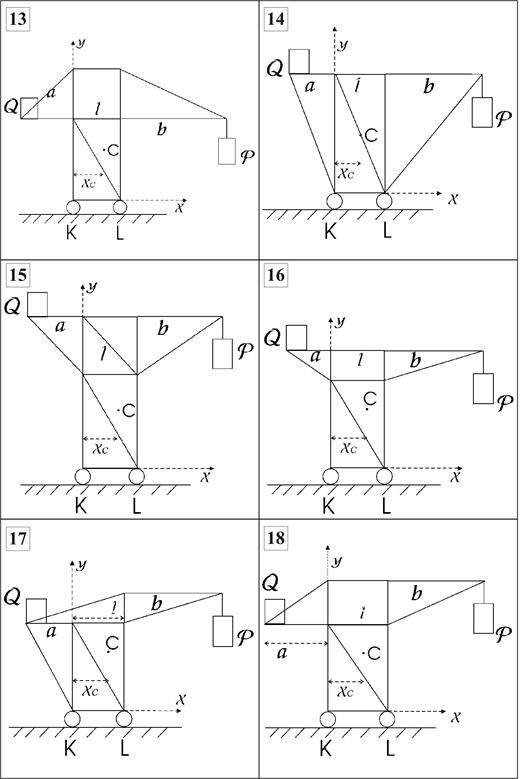
Рис. 3.1 (окончание)       
Т а б л и ц а 3.1

Исходные данные к расчетной работе №1