Число
неизвестных (![]() ,
,![]()
![]() ;
;![]() ) – четыре, то есть больше числа уравнений
равновесия - три, которые можно
составить для этой системы сил. Поэтому для решения данной задачи составную
конструкцию необходимо разделить на две части (т.е. на две подсистемы АС
и СВD) по промежуточному шарниру С (рис.3.6,б).
В месте разделения конструкции необходимо показать соответствующие реакции по
взаимно противоположным направлениям для каждой из частей. Причем, соответствующие
составляющие реакций равны по величине.
) – четыре, то есть больше числа уравнений
равновесия - три, которые можно
составить для этой системы сил. Поэтому для решения данной задачи составную
конструкцию необходимо разделить на две части (т.е. на две подсистемы АС
и СВD) по промежуточному шарниру С (рис.3.6,б).
В месте разделения конструкции необходимо показать соответствующие реакции по
взаимно противоположным направлениям для каждой из частей. Причем, соответствующие
составляющие реакций равны по величине.
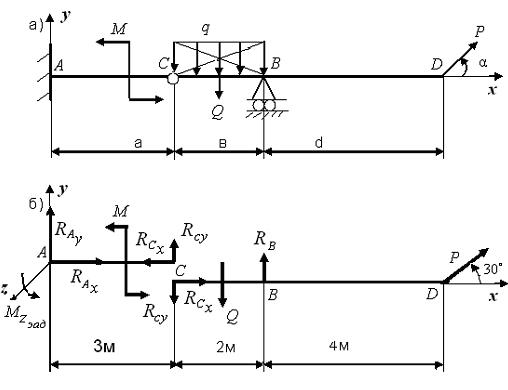
Рис. 3.6
Расчетная схема из двух составных частей показана на рис.3.6,б. Каждая из частей находится в равновесии под действием произвольной плоской системы сил. Для каждой части конструкции можно составить по три уравнения равновесия, приняв ту же систему координат x y (x – по горизонтали вправо, y – по вертикали вверх).
Рассмотрим равновесие правой части (CBD) системы:
CBD ![]()
![]() ,
,![]() ,
, ![]()
![]() .
.
К правой части системы
CBD приложены
неизвестные ![]() ,
,![]() ,
, ![]() -
всего три неизвестных, т.е. число неизвестных (
-
всего три неизвестных, т.е. число неизвестных (![]() ,
,![]() ,
, ![]() )
соответствует числу уравнений равновесия для произвольной плоской системы сил,
приложенных к подсистеме CBD:
)
соответствует числу уравнений равновесия для произвольной плоской системы сил,
приложенных к подсистеме CBD:
1. 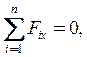 P×cos a×+
P×cos a×+ ![]() = 0;
= 0;
![]()
![]() ;
;
2. 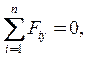 P×sin a- Q -
P×sin a- Q - ![]() +
+![]() =
0;
=
0; ![]()
![]() ;
;
3. 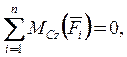 P×sin a
P×sin a ![]() - Q×b/2 +
- Q×b/2 +![]()
![]() =
0.
=
0. ![]()
![]()
Рассмотрим равновесие левой части (AC) системы:
AC![]()
![]() ,
, ![]() ,
, ![]()
![]() .
.
К левой части AC
балки приложены неизвестные силы ![]()
![]() ,
,![]() и момент
и момент![]() . Силы в точке C равны по величине и противоположны по направлению силам
. Силы в точке C равны по величине и противоположны по направлению силам![]() ,
,![]() . Всего в
рассматриваемой задаче к конструкции приложено пять неизвестных сил и момент
. Всего в
рассматриваемой задаче к конструкции приложено пять неизвестных сил и момент ![]() . Для каждой подсистемы (балки) CBD и AC имеем по три уравнения
равновесия, т.е. для системы в целом -
всего шесть уравнений. Задача статически определима, т.е. число неизвестных равно
числу уравнений.
. Для каждой подсистемы (балки) CBD и AC имеем по три уравнения
равновесия, т.е. для системы в целом -
всего шесть уравнений. Задача статически определима, т.е. число неизвестных равно
числу уравнений.
4. 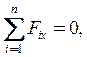
![]() -
-![]() = 0;
= 0; ![]()
![]() ;
;
5. 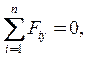
![]() +
+ ![]() = 0;
= 0; ![]()
![]() ;
;
6. 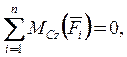 -
- ![]() + M +
+ M + ![]() × а = 0.
× а = 0. ![]()
Из (1): ![]() = - P×cos a = 2 × 0,866 = -1,7 kH.
= - P×cos a = 2 × 0,866 = -1,7 kH.
Из (3): ![]() =
(Q×1-P×6×sin 30°)×2 = (10× 1- 2×6×0,5 ) ×2 = 2kH.
=
(Q×1-P×6×sin 30°)×2 = (10× 1- 2×6×0,5 ) ×2 = 2kH.
Из
(2): ![]() = P sin a - Q +
= P sin a - Q +![]() = 2× 0,5 – 10 +2 = – 7kH.
= 2× 0,5 – 10 +2 = – 7kH.
Из
(4): ![]() =
=
![]() = -1.7 кН.
= -1.7 кН.
Из (5): ![]() = -
= - ![]() = 7
кН.
= 7
кН.
Из (6): ![]() =
+ M +
=
+ M + ![]() × а = 7 + (-7)×3 = -14 kHм.
× а = 7 + (-7)×3 = -14 kHм.
Для проверки полученных результатов можно составить уравнение моментов относительно какой-либо точки или уравнение проекций на ось x или y как для всей конструкции, так и для отдельных частей. Любое из этих уравнений при равновесии и подстановке полученных значений реакций должно рав няться нулю.
Всякая произвольная пространственная система сил может быть заменена эквивалентной ей по силовому воздействию системой, состоящей из силы, равной главному вектору системы сил, приложенного в произвольно выбранном центре приведения, и пары сил с моментом, равным главному моменту системы относительно того же центра приведения.
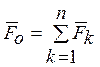 ,
, 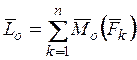 , где О
– центр приведения, принятый за начало декартовой системы координат;
, где О
– центр приведения, принятый за начало декартовой системы координат; ![]() - произвольным
образом ориентированная в пространстве система сил, приложенных к телу.
- произвольным
образом ориентированная в пространстве система сил, приложенных к телу.
Поскольку главный вектор для пары равен нулю, а главный момент сил, составляющих пару, равен моменту пары, то момент пары исчерпывающим образом представляет действие пары на тело.
Условия равновесия произвольной пространственной системы сил
Для равновесия произвольной системы сил, приложенной к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил и главный момент системы сил были равны нулю относительно любого центра приведения, т.е.
![]() = 0,
= 0, ![]() = 0.
Эти условия равновесия называются векторными. Подчеркнем, что центр
приведения
= 0.
Эти условия равновесия называются векторными. Подчеркнем, что центр
приведения ![]() может быть выбран любым.
может быть выбран любым.
Проецируя на оси координат векторные условия равновесия, получаем шесть уравнений равновесия произвольной пространственной системы сил:
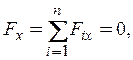
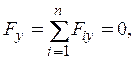
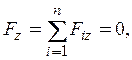
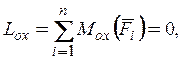
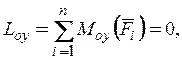
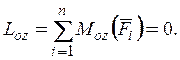
Первые три уравнения являются уравнениями для компонент сил, остальные – уравнениями моментов (при их записи использовано определение момента вектора относительно оси).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.