Статика: Расчетные и курсовые работы по дисциплине "Теоретическая механика", страница 16

5. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА

5.1. Определения, свойства и координаты центра тяжести

Центр тяжести - неизменная точка относительно тела. Поэтому его можно определить как точку, обладающую следующим свойством: если твердое тело закреплено в центре тяжести и приведено в состояние равновесия по отношению к некоторой неподвижной системе отсчета, связанной с Землей, то оно будет сохранять это состояние равновесия при любой ориентации тела относительно вертикали.

Сила тяжести элементарного объема равна произведению массы объема на ускорение   [] (ускорение  при размерах тела, достаточно малых по сравнению с Землей, можно считать для всех частей тела одинаковым):

объемная плотность, единица измерения которой в СИ будет [] .

В случае однородного тела плотность тела одинакова во всех точках

Если тело представляет собой материальную поверхность, то

поверхностная плотность,  - площадь элемента поверхности.

В случае материальной линии (стержень, трос и т.п.)

линейная плотность, - длина элемента линии.

Для однородного тела положение центра тяжести зависит только от геометрической формы тела, а его радиус-вектор и координаты соответственно равны:

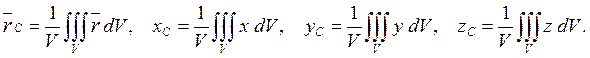         (5.1)

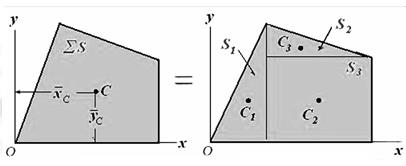
Центры тяжести тонкой однородной пластины  (рис. 5.2) или оболочки и однородного стержня (рис. 5.5) определяются соответственно формулами

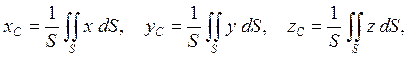                      (5.2)

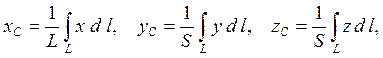                      (5.3)

где    S - площадь поверхности,  L - длина стержня.

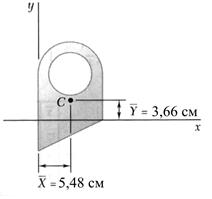
Заметим, что в случае однородного поля силы тяжести  центр тяжести совпадает с центром масс тела и его положение зависит только от того, как распределена в теле масса. Точка  С ¾ центр тяжести (масс) - это геометрическая точка, она может и не принадлежать телу, но всегда с ним связана, например центр тяжести мяча, кольца, и др.

3.2. Методы нахождения центра тяжести

В ряде случаев положение центра тяжести тела можно определить с помощью простых приемов, не прибегая к вычислению интегралов.

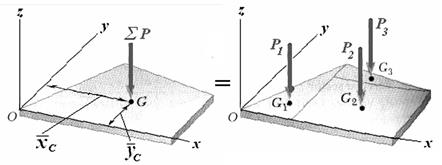
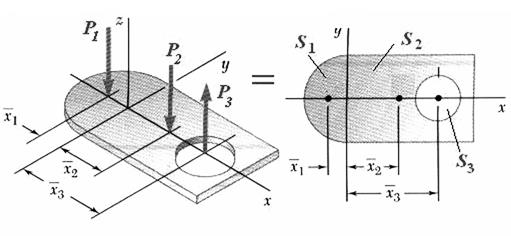
Метод разбиения основан на применении формул для определения положения центра системы параллельных сил (рис. 5.1) в векторной форме или координат точки  С в проекциях на оси координат x, y, z

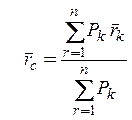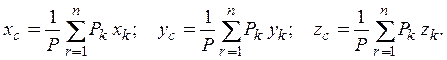,          (5.4)

В формуле (5.4) выражен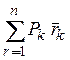ие   называется статическим моментом системы параллельных сил относительно центра  О, а  выражение 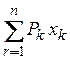, входящее во второе равенство (5.4), ¾ статическим моментом системы параллельных сил относительно плоскости Oyz  и т.д.

В практике расчетов центра тяжести метод разбиения используют, когда тело можно разбить на ряд отдельных частей, для которых веса и положение центров тяжести известны. Метод разбиения можно наглядно проиллюстрировать на нескольких примерах.

Пример 5.1.  Определение центра тяжести однородной пластины (рис.5.1 - 5.4.

◄

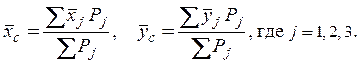Рис.5.1

◄

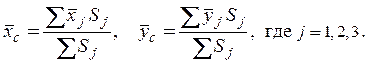Рис. 5.2

Площадь	Форма
	полукруг	-	+	-
	полый прямоугольник	+	+	+
	отверстие круга	+	-	-

Рис. 5.3

Алгебраическая величина площади  частей, из которых составлена  вся область пластины (рис. 5.3), знак минус принимается для вырезов (выемок).

◄

 ◄   

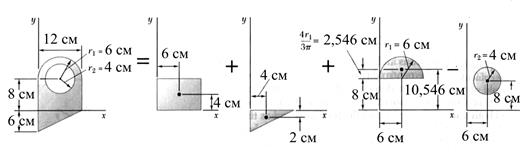
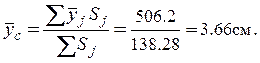	Составляющие     пластины
1	прямоугольник	12×8=96	6	4	+576	+384
2	треугольник	0.5×12×6=36	4	-2	+144	-72
3	полукруг	0.5×p×62 =56.55	6	10,55	+339.3	+596.4
4	полый  круг	-p×42 = -50.27	6	8	-301.6	-402.2
	Итого	=138.28			=757,7	=506,2