Так как
полуэллипсоид вращения симметричен относительно оси x,а плоскость xy - плоскость симметрии тела вращения, то 
В сечении полуэллипсоида вращения
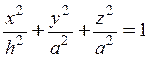плоскостью, параллельной плоскости yOz и отстоящей на расстоянии x от нее, получится круг
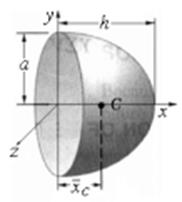
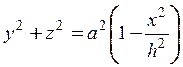. Его
площадь 
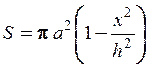, поэтому объем полуэллипсоида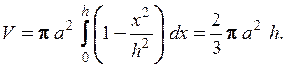 
Так как ось Ox -ось симметрии полуэллипсоида, то его центр тяжести лежит на оси Ox, а координата центра тяжести определяется прямым интегрированием по x и dx по формуле
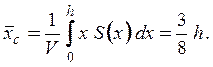Þ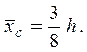 
◄
Рис. 5.11
Т а б л
и ц а 5.1
Центры тяжести простейших тел (тонких однородных пластин и линий)
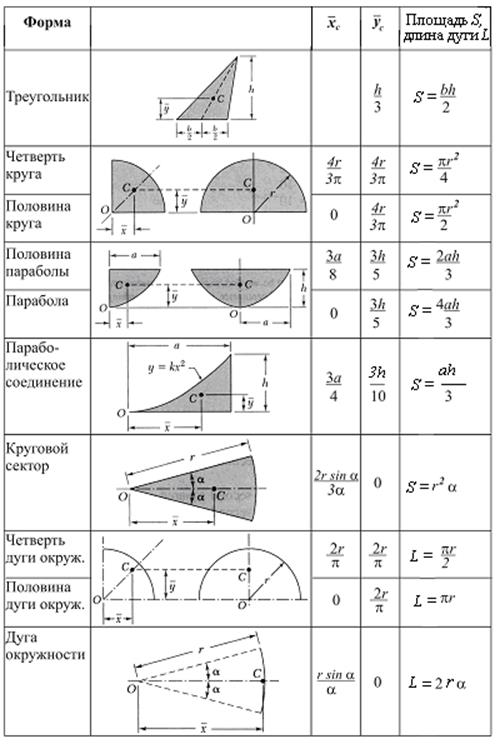
Т а б л и ц а 5.2.
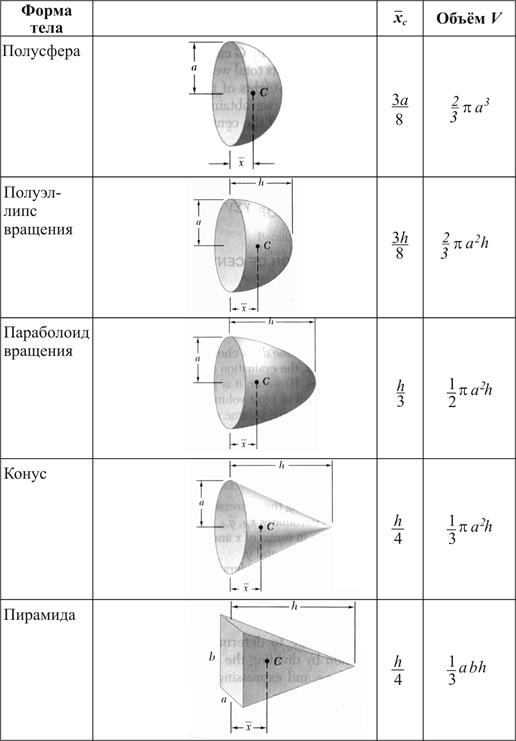
Центры тяжести простейших однородных объемных тел
РАСЧЕТНАЯ РАБОТА №5.
Центр тяжести однородных плоских фигур и линий
Определитьцентры тяжести однородных плоских фигур, линий и объемных тел, схемы которых представлены на рис.5.12, за исключением варианта 21, где приведена схема неоднородного объемного тела (скамейка). Исходные данные (размеры – в метрах) приведены ¾ в табл. 5.3.При выполнении данной расчетной работы рекомендуется пользоваться таблицами для определения центра тяжести простейших тел в зависимости от их геометрической формы
¾ для тонких однородных пластин и линий (стержней) - табл.5.1 и
¾ для однородных объемных тел -табл.5.2 , а также примерами расчета, приведенными в разделе.5.2. Для вариантов 11-21 задача сформулирована конкретно в соответствии с номером варианта на рис.5.12.
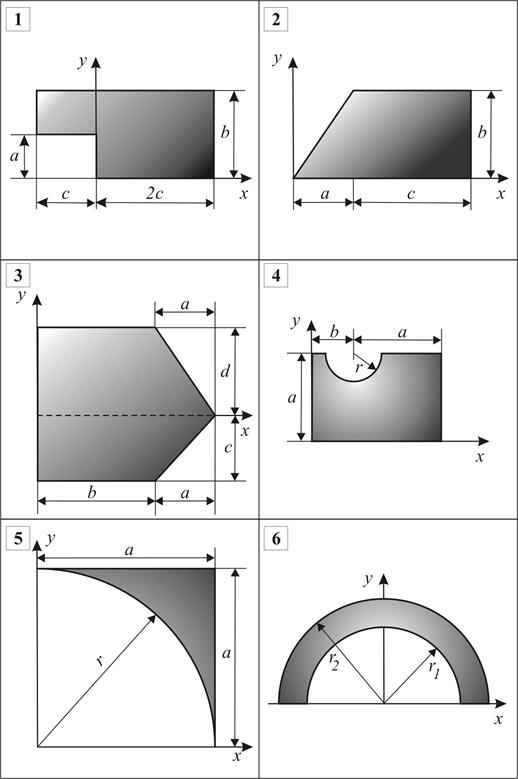
Рис. 5.12. Схемы плоских фигур к расчетной работе №5
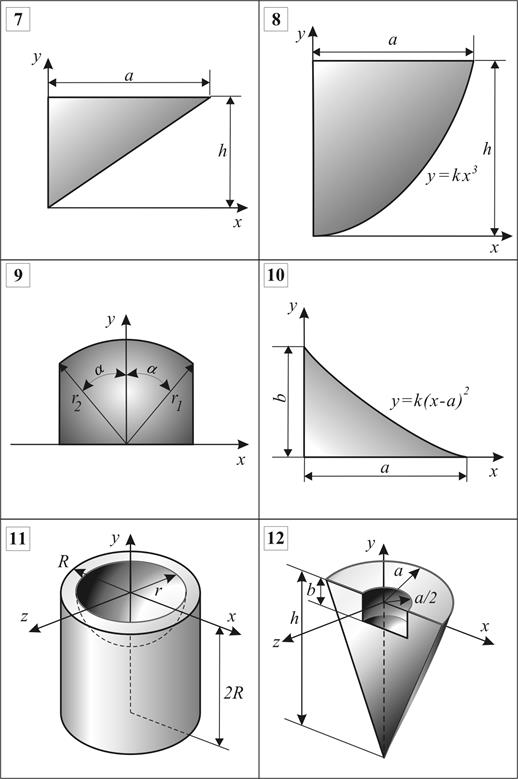
Рис. 5.12 (продолжение)
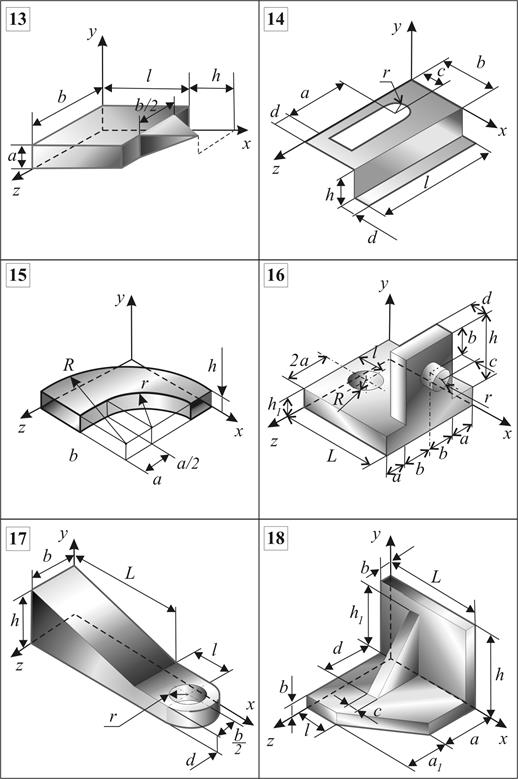
Рис. 5.12 (продолжение)
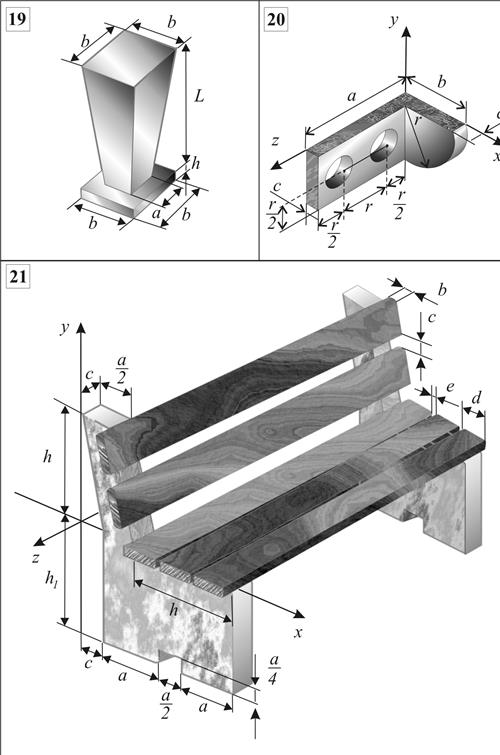
Рис. 5.12 (окончание)
Т
а б л и ц а 5.3
Исходные данные к расчетной работе № 5
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.