Проектный анализ инвестиционного проекта фитнес и спа клуба в Красноярский край, страница 22

Запас финансовой прочности (%)           -      2.50

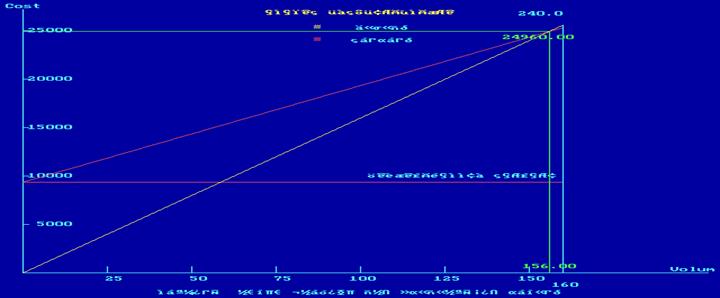
Таким образом, при изменении цены, постоянных и переменных затрат мы наблюдаем изменение в худшую сторону таких показателей, как критический объем производства, прибыль, запас финансовой прочности, операционный рычаг, вклад на покрытие.

7.2. Сложные методы оценки рисков.

Метод дерево решений.

Исходные данные: В момент t=0 производится изучение рыночного потенциала применения роботов для сборки телевизоров, стоимостью 559$ тыс. Вероятность того, что эти исследования дадут благоприятные результаты составляет 85, тогда на этапе t=1 тратится 1059$ тыс., тратится 1100$тыс. на изготовление опытных образцов, вероятность того, что эти образцы себя не зарекомендуются хорошо 37%, тогда на этапе t=2 расходуется 10590$тыс. на строительство завода в дальнейшем. В дальнейшем рассматриваются 3 сценария событий: наихудший – убытки по 2090$ тыс. в течении 5 лет; наиболее вероятное – с доходами по 4090$ тыс. в течении 5 лет; наилучший – доходы по 10090$ тыс. в течении 5 лет, вероятность этих сценариев равна: наихудший – 28; наиболее вероятный – 45; наилучший – 27. Ставка дисконта R=10%

Решение:

Время								Кумулят. вероятность	NPV		Вероятность *NPV
t=0	t=1	t=2	t=3	t=4	t=5	t=6	t=7
								0,15	-559		-84
								0,85*0,37= 0,31	-559- 1059/(1+0,1)=-1471		-459
								0,85*0,63 *0,28=0,150	-16820		-2523
								0,85*0,63 *0,45=0,24	2573		618
								0,8*0,63 *0,27=0,14	21368		2991
Итого:								0,99		543

NPV= -559 -1059/(1,1) -10590/(1,1) -2090/(1,1) -2090/(1,1) -2090/(1,1) -2090/(1,1) -2090/(1,1) = -559 -962 -8752 -1570 -1427 -1298 -1180 -1072 = -16820

NPV= -559 -962 -8719 +3073 +2793+2539+2309+20992573=

NPV=-559-962-8752+7581+6892+6295+5695+5178=21368

Вывод: В результате расчета получаем, что суммарная вероятность, умноженная на NPV, равна 543. Таким образом, данный проект при оценке методом дерева решений вероятнее всего не будет убыточным.

Анализ сценариев.

Проект А.

Сценарий	NPV	Вероятность	Результат
Наилучший	-10090	0,28	-2825
Наиболее вероятный	12090	0,45	5440
Наихудший	35090	0,27	9474

12089   

Среднеквадратическое отклонение

GNPV = (0,28(-10090-12089)^2+0,45(12095-12089)^2+0,27(35090-12089))^1,5=117967

Коэф. вариации

CV= GNPV/ЕNPV=117967/12089=9,76

Проект В.

Сценарий	NPV	Вероятность	Результат
Наилучший	-12090	0,25	-3022
Наиболее вероятный	14090	0,45	6340
Наихудший	40090	0,3	12027

15345

Среднеквадратическое отклонение

GNPV = (0,25(-12090-15345)^2+0,45(14090-15345)^2+0,3(40090-15345))^1,5=137845

Коэф. вариации

CV= GNPV/ЕNPV=137845/15345=8,98

Вывод: Из полученных результатов следует, что проект А менее рискованный т.к GNPV А < GNPV В, а коэф.вариации = 9,76 что является нормой.

Заключение.

В данной курсовой работе были рассмотрены различные методы проектного анализа: коммерческий, технический, экономический, финансовый, анализ возможностей финансирования и анализ рисков проекта. Проведена была оценка инвестиционных проектов с использованием данных методов, в результате по каждой группе сравниваемых проектов был выбран и обоснован наилучший проект - проект, максимизирующий эффективность вложения средств.