Курс лекций по дисциплине “Методы и устройства формирования радиосигналов” (Лекции 1-34. Назначение дисциплины. Радиосигнал и его характеристики. Основные этапы развития радиотехники. Паразитные излучения в формирователях. Электромагнитная совместимость в формирователях), страница 29

Как известно, . Величина  постоянна и зависит только от реактивных сопротивлений резонатора. В то же время . От амплитуды  зависит угол отсечки :

.

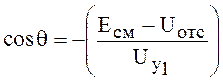Задаваясь значениями , можно найти зависимость  и, следовательно, . Если первоначально , то зависимость  имеет вид (кривая 1):

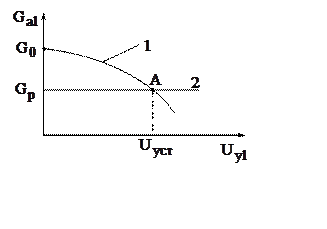
Рис. 5.

Отложив по оси ординат значение  и проведя параллельную прямую оси абсцисс (прямая 2), получим графическое решение уравнения (19) .

Точка А (пересечение двух характеристик) дает значение стационарной амплитуды автоколебаний. Как известно, зависимость  имеет вид:

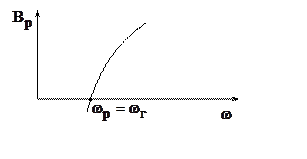
Рис. 6.

Согласно неравенству (23) точка пересечения кривой с осью абсцисс – есть значение генерируемой частоты колебательной системы.

Условие самовозбуждения выглядит так:

, где  - проводимость активного элемента при нулевом напряжении на базе. Если , автогенератор никогда не возбудится.

После определения амплитуды и фазы колебаний, необходимо дать оценку их устойчивости. Из курса радиотехнических цепей известно, что, устойчивому стационарному режиму соответствуют следующие пары неравенств:

1) 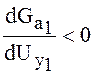, 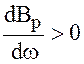;                      2) , .

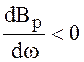Общее условие устойчивости стационарного режима может быть записано в следующем виде:

.

В нашем случае, когда активная проводимость изменяется по нисходящей, а реактивная проводимость по восходящей, то:

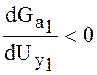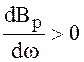, , что соответствует 1 условию устойчивости колебаний автогенератора.

В зависимости от режима работы транзистора можно получить различный характер зависимости .

Если угол отсечки , то зависимость  имеет следующий вид:

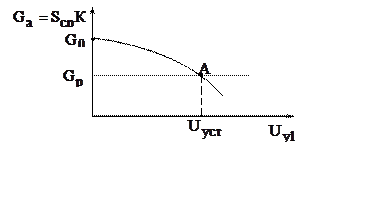
Рис. 7.

На этом графике проведена прямая . Для точки А выполняется уравнение  баланса амплитуд и установившаяся амплитуда колебаний равна .

Приведенная зависимость  соответствует так называемому мягкому режиму самовозбуждения. При этом стационарный режим оказывается устойчивый, а режим покоя  неустойчивым. Поэтому происходит самовозбуждение автогенератора. Действительно, при  отрицательная проводимость, вносимая транзистором, меньше проводимости контура. В результате амплитуда колебаний  начнет уменьшаться, стремясь к установившемуся значению . При  процессы происходят в обратном направлении и амплитуда возрастает до величины .

Построим нагрузочную характеристику активного элемента, т.е. зависимость , где . С этой целью нужно графически решать уравнение для различных :

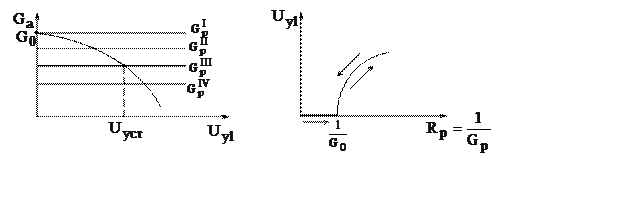
Рис. 8.

Отметим следующие особенности мягкого режима:

1. Плавный вид нагрузочной характеристики, отсутствие скачков амплитуды;

2. Однозначная связь  от ;

3. Монотонный вид зависимости , при котором обеспечивается возможность получения самых малых амплитуд колебаний.

Жесткий режим самовозбуждения возникает в случае, когда смещение на эмиттерном переходе  меньше  зависимость  имеет вид:

Рис. 9.

Оценим устойчивость режимов генерации, возникающей в точках пересечения А и Б.

Раньше было определено, что при нисходящей зависимости  и восходящей  обеспечивается первое условие устойчивости. Следовательно, возникшая генерация с амплитудой  устойчива. Точка Б лежит на восходящей характеристике , т.е. 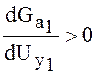. Поскольку в параллельном контуре 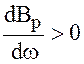, то в точке Б не выполняется ни одно из условий устойчивости.

Рис. 10.

Проанализируем ход нагрузочной кривой при увеличении . Как следует из рисунка, стационарные режимы могут существовать уже при , где  - максимальное значение . Однако, колебания самопроизвольно не возникают, пока не будет выполняться условие самовозбуждения. Таким образом, при увеличении  колебания возбуждаются скачком до амплитуды  при . С дальнейшим ростом  амплитуда возрастает плавно. Если теперь, когда существуют колебания, уменьшать , то при  срыва автогенерации не будет, т.к. условие существования режима выполняется, а выполнение условия самовозбуждения не требуется. Колебания прекратятся скачком при .

Обратим внимание на особенности автогенератора, работающего в жестком режиме самовозбуждения:

1. Скачкообразный характер возбуждения и срыва колебаний.

2. Наличие петли гистерезиса в нагрузочной характеристике.

3. Вид зависимости , при которой не возможно получить малые амплитуды.