Курс лекций по дисциплине “Методы и устройства формирования радиосигналов” (Лекции 1-34. Назначение дисциплины. Радиосигнал и его характеристики. Основные этапы развития радиотехники. Паразитные излучения в формирователях. Электромагнитная совместимость в формирователях), страница 28

С помощью формулы (1) определим выходной ток , протекающий через АЭ и колебательную систему (резонатор):

.                                                       (5)

Разделив левую и правую часть равенства (5) на , получим основное уравнение АГ:

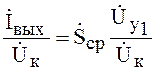.                                                      (6)

Учитывая (2) и (3), перепишем выражение (6):

.                                                      (7)

Величины, входящие в уравнение (7) можно выразить в следующей форме:

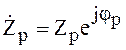, , .                           (8)

Учитывая (8), уравнение (7) запишем в виде:

,                                     (10)

,  .                               (11)

Здесь  - суммарный фазовый сдвиг.

Уравнение (10) носит название баланса амплитуд, а (11) – уравнение баланса фаз.

В уравнении (10) от амплитуды колебаний зависит только .

Следовательно, уравнение (10), которое выполняется только для вполне определенной амплитуды колебаний, позволяет определить амплитуду установившихся колебаний автогенератора.

Поскольку в уравнении баланса фаз (11) каждый из фазовых сдвигов   зависит от частоты, то существует значение установившейся частоты колебаний, для которой это уравнение выполняется. Следовательно, уравнение баланса фаз позволяет определить частоту генерируемых колебаний.

Рассмотрим выражение (7) с иной точки зрения и запишем его в следующей форме:

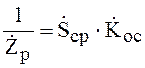.                                                   (12)

Введем обозначения:

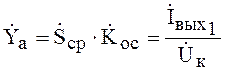        (13)                             (14)

При правильно выбранной положительной обратной связи у АГ, также как и у ГВВ:

.                                                     (15)

Поэтому с учетом (15) выражение (14) можно переписать в виде:

.                                                    (16)

Следовательно, комплексное уравнение (12) примет вид:

,                                                       (17)

.                                                     (18)

Уравнение (18) положило начало методу эквивалентных схем, который эффективно применяется при анализе не только АГ с внешней обратной связью, которыми являются транзисторные и ламповые АГ, но и АГ с внешней обратной связью, так называемых, ,,диодных АГ”, а также при изучении явлений синхронизации, самосинхронизации, затачивания частоты и т.д.

Соотношение (17) может быть зависимо в виде двух равенств:

,     (19)         и          ,     (20)

Правая часть выражения (19) характеризует отрицательную проводимость, вносимую транзистором, а правая часть – положительную проводимость контура. Уравнение (20) – это уравнение компенсации реактивных проводимостей. Естественно, что генерация возникает при равенстве этих проводимостей.

На сравнительно низких частотах () и в автогенераторах, использующих высокодобротный колебательные системы с полным основанием, можно считать:

, а также                                              (21)

,  ,  .

При условии (21) уравнение баланса фаз вырождается в равенство:

.                                                            (22)

Следовательно, колебания в АГ возникают на резонансной частоте контура, что, в свою очередь, позволяет находить частоту колебаний из уравнения:

.                                                    (23)

 - реактивные сопротивления контура, подключенного к транзистору.

Учитывая вещественный характер коэффициента обратной связи, непосредственно из (23) получим два условия возникновения колебаний в трехточечной схеме:

1) ;  ;  ;                                  .

2) ;  ;  ;                                  .

Эквивалентная схема АГ, построенная в соответствии с условием 1, получила название ,,индуктивная трехточка” и имеет вид:

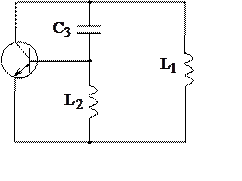
Рис. 3.

А схема, выполненная с учетом условия 2 называется ,,емкостной трехточкой”:

Рис.4.

Наиболее распространена емкостная трехточка из-за хороших фильтрующих свойств. Индуктивную трехточку применяют в АГ, перестраиваемых по частое: в возбудителях передатчиков и гетеродинах приемников.

Для нахождения стационарной амплитуды автоколебаний и частоты автогенерации, необходимо знать зависимости отрицательной проводимости активного элемента от амплитуды возбуждения  и реактивной проводимости  резонатора от частоты .