![]() , (4.23)
, (4.23)
где m – масса поступательно движущихся частей механизма, кг;
ρ – радиус приведения.
Если же известен маховой момент GD², то момент инерции можно рассчитать по следующей формуле;
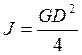 . (4.24)
. (4.24)
Суммарный момент инерции электропривода определяется следующим образом:
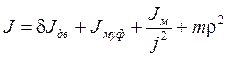 , (4.25)
, (4.25)
где δ=1,15÷1,3 – коэффициент, учитывающий момент инерции вращающихся масс передаточного механизма;
Jдв – момент инерции ротора двигателя;
Jмуф – момент инерции соединительной муфты, тормоза и других частей механизма, непосредственно связанных с валом двигателя;
Jм – момент инерции вращающихся частей механизма;
j – передаточное число редуктора;
m – масса поступательно движущихся частей механизма, кг;
ρ – радиус приведения.
5. РАСЧЕТ И ПОСТРОЕНИЕ УПРОЩЕННОЙ
НАГРУЗОЧНОЙ ДИАГРАММЫ ЭЛЕКТРОПРИВОДА
Нагрузочная диаграмма электропривода представляет собой зависимость электромагнитного момента М, тока I или мощности Р от времени. В тех случаях, когда момент и ток связаны линейной (или примерно линейной) зависимостью, обычно нагрузочную диаграмму строят для момента, который определяют из основного уравнения движения электропривода:
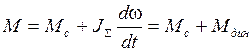 , (5.1)
, (5.1)
где Мс – статический момент на валу двигателя;
Мдин – динамический момент электропривода;
JΣ – суммарный момент инерции электропривода, определяемый по (3.),кг·м².
Динамический момент электропривода Мдин определяют предварительно приближенно, принимая линейным закон изменения скорости, т.е.
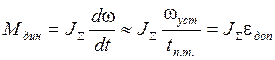 , (5.2)
, (5.2)
где ωуст – установившаяся скорость двигателя на данном участке скоростной диаграммы, рад/с;
tп.т. – время пуска (торможения), с;
εдоп – допустимое угловое ускорение (замедление), рад/с
Допустимое угловое ускорение εдоп связано с допустимым линейным ускорением αдоп соотношением
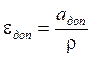 , (5.3)
, (5.3)
где ρ – радиус приведения, м.
Время разгона (торможения) tп.т. можно определить из следующего соотношения
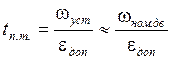 .
(5.4)
.
(5.4)
На каждом интервале нагрузочной диаграммы момент двигателя рассчитывается по формуле
![]() . (5.5)
. (5.5)
В соответствии с формулой (5.5) рассчитывается и строится упрощенная нагрузочная диаграмма электропривода (рис. 5.1).
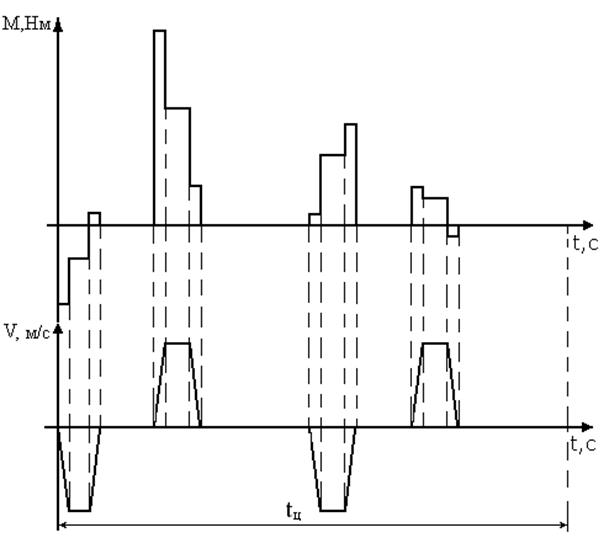

Упрощенная нагрузочная диаграмма используется для предварительной проверки двигателя по нагреву, пусковой и перегрузочной способностям.
Для проверки двигателя по нагреву используется несколько методов: метод средних потерь и методы эквивалентных величин (тока, момента и мощности).
Наиболее точным является метод средних потерь. Сущность этого метода заключается в нахождении средних потерь двигателя ΔРср при заданном графике нагрузки и сравнении с найденных таким образом средних потерь с номинальными потерями, на которые рассчитан двигатель при длительной работе. В методе средних потерь предполагается, что при равенстве потерь ΔРср= ΔРном двигатель будет работать с допустимой для него температурой.
Таким образом, условием правильного выбора двигателя по нагреву будет следующее выражение:
ΔРср≤ΔРном. (5.6)
Средние потери мощности вычисляются следующим образом:
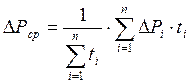 , (5.7)
, (5.7)
где ΔРi – потери мощности на i-ом интервале нагрузочной диаграммы;
ti – продолжительность i-го интервала.
На интервалах с установившейся скоростью потери мощности можно рассчитывать по формуле
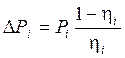 , (5.8)
, (5.8)
где Рi – мощность на i-ом интервале нагрузочной диаграммы, определяемая как
![]() , (5.9)
, (5.9)
где Мi – момент на i-ом интервале нагрузочной диаграммы;
ωi – угловая скорость двигателя на i-ом интервале;
ηi – КПД двигателя на i-ом интервале при частичной загрузке
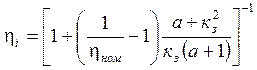 , (5.10)
, (5.10)
где α – коэффициент постоянных потерь
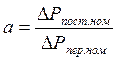 ; (5.11)
; (5.11)
кз – коэффициент загрузки
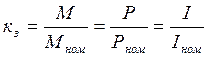 . (5.12)
. (5.12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.