Основы эргономики: Методическое пособие по выполнению практических работ, страница 19

Изменяя значения логических условий, можно получить различные варианты последовательности работы алгоритма, число которых равно 2^N, где N – количество логических условий.

Работа человека-оператора включает в себя обычно систему таких алгоритмов.

С помощью анализа алгоритмов деятельности оператора решается целый ряд задач:

– исследование влияния сложности алгоритма на качество работы человека-оператора;

– распределение функций между человеком и машиной;

– разработка алгоритмов работы человека-оператора при проектировании систем «человек-машина» и др.

Анализ схемы алгоритма позволяет получить некоторые количественные характеристики трудовой деятельности оператора: показатели стереотипности, логической сложности,  скорости переработки информации, динамической интенсивности.

Показатель стереотипности оценивается по наличию в алгоритме непрерывных последовательностей без логических условий, а также по длительности этих последовательностей. Этот показатель определяется по формуле

 ,                                            (1)

где       – вероятность появления таких групп;

– число последовательных элементов в группе без логических усло-  вий из 1, 2, ..., k элементов.

Показатель стереотипности достигает максимального значения, равного k, когда в алгоритме нет логических условий, т. е. последовательность дей-ствий оператора однозначно детерминирована и не зависит ни от каких условий. Минимально возможное значение этого показателя равно 1; оно получается в том случае, если после каждого «оператора» следует логическое условие. Следовательно, в этом случае      = l,      = 1/k, Z = 1. Деятельность оператора при этом имеет максимальное число возможных вариантов действий, т. е. низкую стереотипность.

Показатель логической сложности определяется выражением

,                                             (2)

где     – вероятность появления таких групп. Этот показатель определяет необходимость изменения системы действий в различных вариантах условий выполнения производственных процессов. Он дает характеристику, обратную стереотипности, и может быть использован для оценки динамического компонента деятельности оператора. Возможные пределы изменения 0 ≤ L ≤ m;

              – число проверяемых логических условий в группе из 1, 2, ..., т таких условий.

Энтропия «операторов» всех видов, т. е. среднее количество информации, перерабатываемое человеком-оператором при выполнении управляющих действий, вычисляется по формуле

Но =

Рi log Рi,

                                                                 (3)

где P_i – вероятность 1, 2, ..., i-го вида «оператора»;

        х – число операторов i-го вида в алгоритме.

Энтропия логических условий, т.е. среднее количество информации, перерабатываемое человеком-оператором при проверке логических условий, вычисляется по формуле

Рj log Рj,

Нл =

                                                     (4)

где r – число логических условий  j-го вида в алгоритме;

     P_j – вероятность 1, 2, ..., j-го вида логического условия.

Для вычисления значений энтропии «операторов» и логических условий можно принять вероятности для всех «операторов» и логических условий равными. Тогда формулы (3) и (4) примут вид:

  H₀  = log₂ х;      H_л = log₂ r,                                   (5)

где x и r – общее число «операторов» и логических условий.

Средняя информация по всем шагам трудового процесса равна сумме энтропий «операторов» и логических условий. Последний показатель является характеристикой неопределенности ожидания различных членов алгоритма.

Средняя скорость переработки информации

     S = 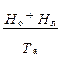,                                                 (6)