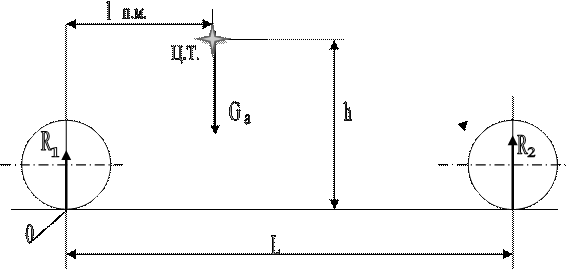
Рис.1.3. Расчетная схема к задаче
Таким образом на переднюю ось автомобиля приходится 6774 кг , а на заднюю ось – 4951 кг массы автомобиля.
ЗАДАЧА 3
Вес автомобиля равен 55 кН, а база L = 4 м. Центр тяжести находится на расстоянии 1,2 м от оси заднего моста и на высоте 0,9 м от полотна дороги. При движении ведущие колеса развивают силу тяги равную 11 кН. Определить нормальные реакции на переднем и заднем мостах в статическом состоянии и при равномерном движении автомобиля с малой скоростью.
Решение: составим расчетную схему (см. рис.1.4).
Для определения реакций в статическом положении составим уравнение моментов всех сил действующих относительно точки О (при этом сила тяги Рт и момент сопротивления Мf отсутствуют):
![]() R2·L -Ga·(L
- lз.м.)
= 0; отсюда
R2·L -Ga·(L
- lз.м.)
= 0; отсюда 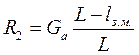 =55
=55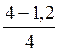 =38,5 кН, тогда R1 = Ga - R2 = 55 –
38,5 = 16,5 кН.
=38,5 кН, тогда R1 = Ga - R2 = 55 –
38,5 = 16,5 кН.
При движении автомобиля создается опрокидывающий момент Мƒ = Рт·hц.т., который догружает заднюю ось и разгружает переднюю. Тогда уравнение моментов примет вид:
R2·L -Ga·(L - lз.м.) - Рт·hц.т. = 0; отсюда
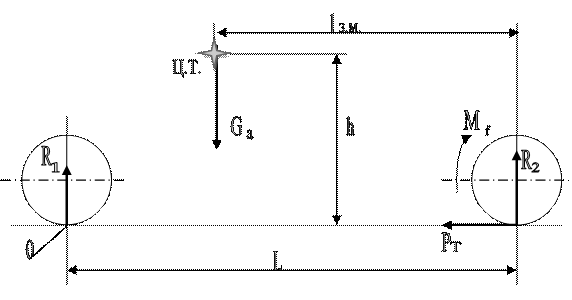
Рис.1.4. Расчетная схема к задаче
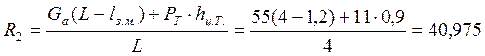 кН,
а реакция передней оси составит R1 = 55 –
40,975 = 14,025 кН.
кН,
а реакция передней оси составит R1 = 55 –
40,975 = 14,025 кН.
ЗАДАЧА 4
Рассчитать нормальные реакции на осях автомобиля, а также коэффициенты перераспределения нагрузки на оси, если его вес равен 55 кН; база – 4 м; продольная координата центра тяжести от оси заднего моста – b = 1,2 м, а высота 0,9 м. Автомобиль движется по сухому асфальтобетонному покрытию с продольным коэффициентом сцепления равным φx = 0,8 и полным использованием сцепления ведущими колесами.
Решение: составим расчетную схему рис. 1.5. Максимальное тяговое усилие по сцеплению при движении автомобиля составит Рт = Gсц·φx. Сцепной вес принимаем равным нагрузке, приходящейся на ведущую ось при статическом положении автомобиля. Для определения этой нагрузки составим уравнение моментов всех сил при статическом положении автомобиля относительно точки «О» (при этом сила тяги Рт и момент сопротивления Мf отсутствуют), т.е.
![]() R2·L -Ga·(L
- lз.м.)
= 0; отсюда
R2·L -Ga·(L
- lз.м.)
= 0; отсюда 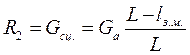 =55
=55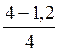 =38,5 кН; тогда Рт
= 38,5·0,8 = 30,8 кН.
=38,5 кН; тогда Рт
= 38,5·0,8 = 30,8 кН.
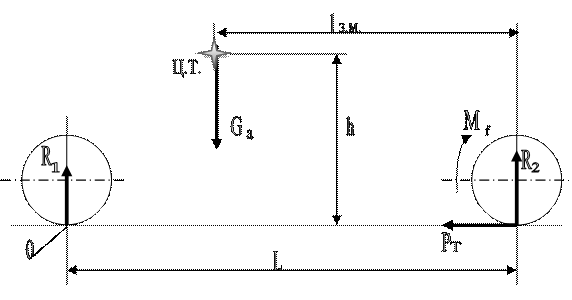
Рис.1.5. Расчетная схема к задаче
Составим уравнение моментов
относительно точки «О» при движении автомобиля (см. рис. 1.5): ![]() . Соответственно нагрузка,
приходящаяся на ведущую ось при движении автомобиля, будет равна:
. Соответственно нагрузка,
приходящаяся на ведущую ось при движении автомобиля, будет равна:
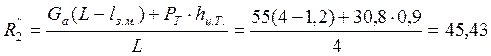 кН, а
на переднюю ось соответственно –
кН, а
на переднюю ось соответственно – ![]() 55 – 45,43 = 9,57
кН.
55 – 45,43 = 9,57
кН.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.