



































М-8. МЕТОД СИЛ
8.0. Введение в модуль
Основными целями модуля являются:
- получение формул для определения внутренних усилий в произвольной плоской статически неопределимой стержневой конструкции;
- рассмотрение особенностей определения внутренних усилий с учетом симметрии плоской статически неопределимой стержневой конст- рукции;
- получение матричных формул для определения внутренних усилий в плоской статически неопределимой стержневой конструкции;
- рассмотрение особенностей определения перемещений в плоской статически неопределимой стержневой конструкции.
Структура изучаемого модуля включает следующие учебные элементы:
1. Расчет методом сил произвольной плоской статически неопределимой стержневой конструкции.
2. Поверки метода сил.
3. Особенности расчета методом сил симметричных плоских статически неопределимых стержневых конструкций.
4. Матричная форма расчета методом сил плоских статически неопределимых стержневых конструкций.
5. Определение перемещений в плоских статически неопределимых стержневых конструкциях.
При изучении учебных элементов рекомендуется использование следующей литературы: [1, c.309 – 391]; [3, c.193 – 249]; [4, c.251 – 257, 293304, 341-354]; [5, c.238-287 – 48].
8.1. Расчет методом сил произвольной плоской статически неопреде-
лимой стержневой конструкции
8.1.1. Постановка задачи
Задана произвольная плоская статически-неопределимая стержневая конструкция (рис. 8.1), для которой считаются известными все размеры геометрической схемы и поперечных сечений стержней
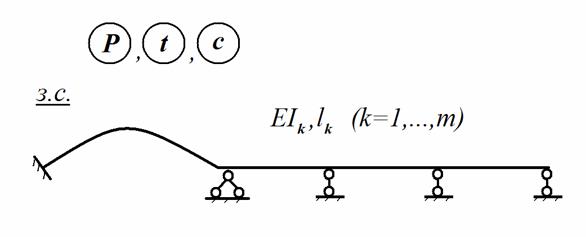
Рис. 8.1
Степень полной статической неопределимости заданной системы равняется
Л = n .
На заданную систему действуют произвольная нагрузка, температурные изменения (температура) и осадка опор, показанные на рис.8.1 условными буквенными обозначениями: P – нагрузка, t – температура, c – осадка опор. Заданная конструкция считается линейно деформируемой системой.
8.2.2.Основная система и канонические уравнения
В основе расчета стержневых конструкций методом сил лежит пере- ход от заданной статически-неопределимой системы к расчету эквива- лентной статически-определимой системы. Эквивалентность двух систем должна состоять в одинаковости внутренних усилий (статическая экви- валентность) и одинаковости перемещений (кинематическая эквива- лентность). Такая эквивалентная статически определимая система и назы- вается основной системой метода сил.
Для получения основной системы из заданной системы сначала удаляют все лишние связи (рис. 8.2)
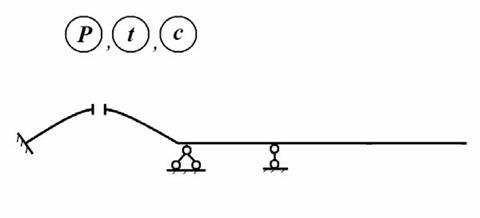
Рис. 8.2
так, чтобы преобразованная система была геометрически неизменяемой с необходимым числом связей и, следовательно, статически-определимой. Поскольку возможны различные схемы удаления лишних связей в задан- ной системе, то возможно получение нескольких вариантов статически- определимых систем.
Статическая эквивалентность полученной статически- определимой системы заданной системе достигается приложением к ней в качестве дополнительных внешних воздействий реакций удаленных лиш-
них связей
X 1 ,..., X n
(рис. 8.3,а)
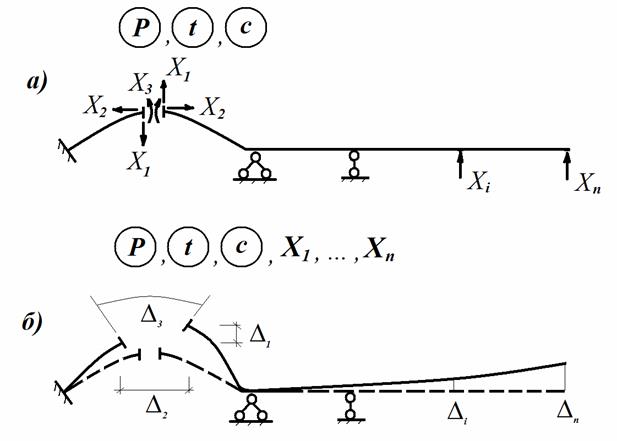
Рис. 8.3
При дальнейшем расчете эти реакции подлежат первоочередному определению и поэтому они называются основными неизвестными ме- тода сил. И, поскольку, основные неизвестные являются реакциями, то они имеют статическую природу.
Для достижения кинематической эквивалентности двух систем вводятся условия обращения в ноль полных перемещений (рис. 5.3,б)
D1 = 0,...,Dn = 0 , (8.3)
возникающих в статически-определимой системе по направлению основ- ных неизвестных. Так как эти перемещения порождаются основными не- известными и заданными внешними воздействиями, то они являются функциям этих величин и условия (8.3) можно записать в следующем виде
|
|
,..., X n
,P,t ,c) = 0,
.....................................
(8.4)
|
|
|
|
,P,t ,c) = 0.
Поскольку заданная стержневая конструкция считается линейно деформируемой системой, то дополнительные условия (8.4), согласно принципу суперпозиции, принимают вид
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.