Метод сил, страница 12

С учетом (8.28), система канонических уравнений (8.27) распадается на две независимые подсистемы уравнений. Первая подсистема уравнений содержит только симметричные основные неизвестные (рис.8.9.а)

11     1           12      2            13      3             1P

d  X  + d  X   + d  X  + D   = 0

21     1            22      2            23      3             2 P

d   X  + d   X   + d   X  + D    = 0

31     1           32       2            33      3             3 P

d  X  + d   X   + d   X  + D    = 0

а вторая - только антисимметричные основные неизвестные (рис.8.9.б)

44       4            45       5            46       6             4 P

d   X   + d   X  + d   X   + D    = 0

54       4            55       5            56       6             5 P

d   X   + d   X  + d   X   + D    = 0

64       4            65       5            66       6              6 P

d   X   + d   X  + d   X   + D    = 0

Таким образом, группировка основных неизвестных и искусственное выделение симметричных и антисимметричных основных неизвестных по- зволяет получить рациональную основную систему в общем случае. Сим- метричную стержневую систему, в которой для образования рациональной

основной  системы  требуется  применять  группировку  основных  неизвестных, будем называть симметричной системой общего вида.

8.3.4. Особенности расчета симметричных систем на симметричные и антисимметричные нагрузки

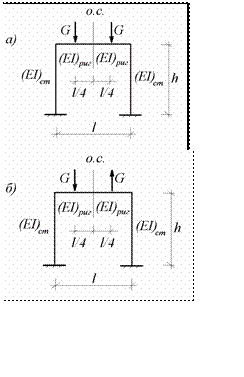
Рассмотрим  особенности  такого  расчета  на  примере  симметричной одноэтажной однопролетной рамы, загруженной   в одном случае симмет- ричной нагрузкой (рис.8.10.а) и в другом случае – антисимметричной на- грузкой (рис.8.10.б)

Рис.8.10

Рациональная основная система метода сил показана на рис.8.6.а               и ее выбор не зависит от схемы нагружения. Поэтому, как в случае симметричной  схемы  нагружения,  так  и  в  случае  антисимметричной  схемы  нагружения  для  расчета  рамы  будет  использоваться  система  канонических уравнений (8.26).

Для  определения  свободных  членов  канонических  уравнений  рассмотрим грузовые состояния основной системы и построим грузовые эпюры изгибающих моментов (рис.8.11)

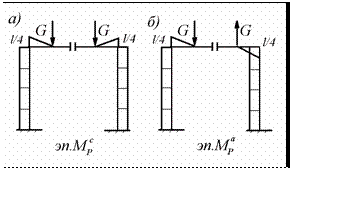Рис.8.11

При  действии  симметричной  нагрузки  грузовая  эпюра  изгибающих моментов  имеет симметричное очертание (рис.8.11.а). Поэтому свободный

1P

член

D   , получаемый  при перемножении симметричной грузовой эпюры

M P       с   единичной   эпюрой

m1 ,   имеющей   антисимметричное   очертание

(рис.8.6.б), будет тождественно равен нулю

D1P   º 0

(8.29)

D

3 P

Два других свободных члена          2 P

и  D    , получаемые при перемноже-

нии  при  перемножении  симметричной  грузовой  эпюры  M P

(рис.8.11.а)  с

единичными      эпюрами

m2 ,

m3 ,   имеющими      симметричное      очертание

(рис.8.6.в), будут отличными от нуля

D2 P   ¹ 0,

D3 P   ¹ 0

Тогда решая систему канонических уравнений (8.26), с учетом (8.29),

получим, что антисимметричное основное неизвестное

X1  º 0 .

X1   будет равно

Обобщая полученный результат, можно сделать первый вывод, связанный с особенностями расчета методом сил симметричных стержневых систем. При  расчете  таких  систем  на  действие  симметричной  нагрузки  все  анти- симметричные основные неизвестные метода сил тождественно равны ну- лю.

При действии антисимметричной нагрузки грузовая эпюра изгибающих  моментов      имеет  антисимметричное  очертание  (рис.8.11.б). Поэтому

свободные  члены D2 P

и  D3 P  ,  получаемые  при  перемножении  антисиммет-