Строительство и архитектура \ Строительная механика

Метод сил, страница 11


Л = 6,


Л1  = 6,


Л 2  = 0 .


и все лишние связи содержатся в опорных закреплениях. Расчет такой ра- мы,  при  любой  схеме  удаления  лишних  связей  для  получения  основной системы  метода сил, связан с составлением и решением шести канониче- ских уравнений


11     1           12       2           13      3           14       4           15      5           16       6            1P
 
d  X  + d  X   + d  X  + d  X   + d  X  + d  X   + D   = 0

21     1            22       2            23      3            24       4            25       5            26      6             2 P
 
d   X  + d   X   + d   X  + d   X   + d   X  + d   X   + D    = 0

31     1           32       2            33      3            34       4            35      5            36       6             3 P
 
d  X  + d   X   + d   X  + d   X   + d   X  + d   X   + D   = 0

41     1            42      2            43      3            44      4            45      5            46       6             4 P
 
d   X  + d   X   + d   X  + d   X   + d   X  + d   X   + D   = 0

51     1            52       2            53      3            54      4            55      5            56      6             5 P
 
d  X  + d   X   + d   X  + d   X   + d   X  + d   X   + D   = 0

61     1            62       2            63      3            64       4            65      5            66       6             6 P
 
d  X  + d   X   + d   X  + d   X   + d   X  + d   X   + D    = 0


(8.27)


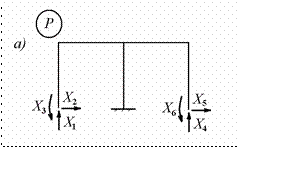
Образуем основную систему, соблюдая признаки симметрии стерж- невой   конструкции.   Для   этого   удалим   крайние   опорные   закрепления (рис.8.8.а)

Рис.8.8

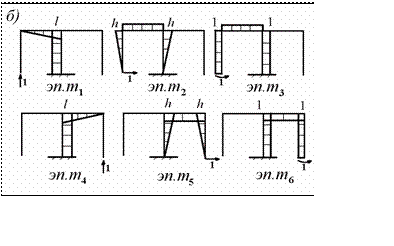
Однако  если  рассмотреть  все  единичные  состояния  (рис.8.8.б),  то  из  построенных единичных эпюр изгибающих моментов, очевидно, что ни один из побочных коэффициентов не равен нулю


ik
 
d   ¹ 0


( i ¹ k ;


i ,k = 1,...,6 )


Следовательно, сохранение свойств симметрии геометрических  раз- меров,  схем узловых  соединений  и жесткостных  характеристик  не позво- лило  получить  для  рассматриваемой  симметричной  рамы  более  общего вида  рациональную  основную  систему  метода  сил,  как                                                                                                 это  произошло  в частном случае. Причиной этого является отсутствие автоматического раз- деления  основных  неизвестных  метода  сил  на  симметричные  и  антисим- метричные величины.


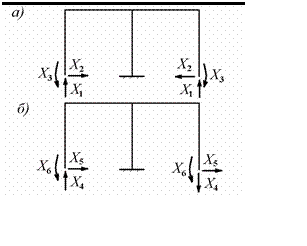Поэтому для симметричных систем общего вида применяют группи- ровку   однотипных   основных   неизвестных   и   искусственное   выделение симметричных и антисимметричных составляющих. Такое разделение для рассматриваемой рамы показано на рис.8.9

Рис.8.9


В этом случае единичные эпюры изгибающих моментов


m1 , m2 ,m3 , связан-


ные  с  симметричными  основными  неизвестными  (рис.8.9.а),  будут  иметь симметричные   очертания.    Единичные    эпюры   изгибающих    моментов

m4 , m5 ,m6 ,   связанные   с   антисимметричными   основными   неизвестными

(рис.8.9.б), будут иметь антисимметричные очертания. Следовательно, все побочные  коэффициенты  системы  канонических  уравнений  (8.26),  полу- чаемые при перемножении симметричных единичных эпюр с антисиммет- ричными и наоборот, тождественно равны нулю


ik            ki
 
d    = d   º 0


( i = 1,2,3;


k = 4,5,6 )


(8.28)


Скачать файл