Л= 3,
Л1 = 3,
Л2 = 0 .
и все лишние связи содержатся в опорных закреплениях. Расчет такой ра- мы, при любой схеме удаления лишних связей для получения основной системы метода сил, связан с составлением и решением трех канонических уравнений
d11 X1 + d12 X 2 + d13 X 3 + D1P = 0
d 21 X1 + d 22 X 2 + d 23 X 3 + D 2 P = 0
d 31 X1 + d 32 X 2 + d 33 X 3 + D3 P = 0
(8.25)
Первый вариант основной системы может быть получен удалением всех лишних связей на одной из рамных опор, например, правой (рис.8.5.а)
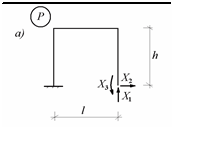
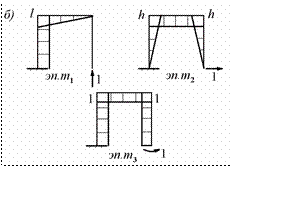Рис.8.5
Выясним, к какой разновидности основных систем метода сил относится выбранный вариант основной системы. Для этого проанализируем с по- мощью формулы Максвелла-Мора, какие значения могут принимать по- бочные коэффициенты канонических уравнений (8.25). При анализе вели- чин коэффициентов ограничимся учетом влияния только изгибных дефор- маций
3
= å ò
mi m j
d ij ds .
k =1 l
EI z
Рассмотрим три единичных состояния основной системы и построим эпюры соответствующих единичных изгибающих моментов (рис.8.5.б). Очертания этих эпюр не имеют никаких характерных особенностей и, оче- видно, что при их перемножении согласно правилу Верещагина ни один из побочных коэффициентов в ноль не обращается
dij ¹ 0 (i ¹
j, i, j = 1,2,3).
Поэтому для определения основных неизвестных, согласно выбран- ному варианту основной системы метода сил, нужно совместно решать три канонических уравнения системы (8.25). Следовательно, рассмотренный первый вариант основной системы является обычным и не приносит ника- ких упрощений при составлении и решении канонических уравнений.
Второй вариант основной системы может быть получен удалением трех лишних связей введением сквозного разреза в сечении, лежащем на оси симметрии рассматриваемой рамы (рис.8.6.а)
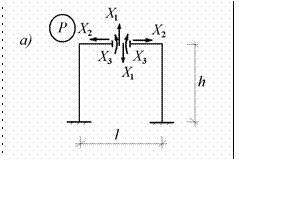
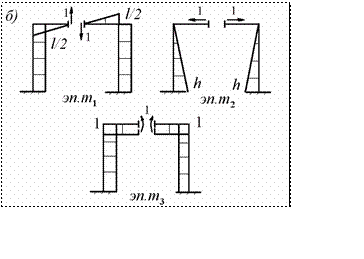Рис.8.6
При этом, в отличие от первого варианта, основная система удовлетворяет признакам симметрии.
Как и в первом случае, проведем анализ величин побочных коэффициентов, используя для этого формулу Максвелла-Мора. Для этого опять рассмотрим три единичных состояния и построим эпюры единичных изги- бающих моментов (рис.8.6.б). Однако в этом случае среди единичных эпюр появились эпюры, имеющие антисимметричное очертание (эп. m1) и симметричные очертания (эп. m2, m3). Это является следствием того, что три лишних связи были удалены в сечении, лежащем на оси симметрии, и
основные неизвестные сами разделились на антисимметричные
X1 и сим-
метричные величины
X 2 , X 3 .
Поэтому все побочные коэффициенты, получаемые при перемноже- нии эпюр симметричного и антисимметричного очертаний, будут тождест- венно равны нулю
d12 = d 21 = d13 = d 31 º 0 .
В этом случае система канонических уравнений (8.25) распадается на две подсистемы уравнений
|
|
|
(8.26)
Следовательно, второй вариант основной системы позволяет независимо найти антисимметричное основное неизвестное и симметричные основные неизвестные.
Таким образом, сохранение свойств симметрии при образовании ос- новной системы и разделение неизвестных на симметричные и антисим- метричные величины позволяет получить рациональную основную систему метода сил. Симметричные статически неопределимые стержневые конструкции, для которых удается удалить все лишние связи в сечениях, принадлежащих оси симметрии и, как следствие этого, получить автоматическое разделение основных неизвестных метода сил на симметричные и антисимметричные величины, будем называть симметричными системами частного вида.
8.3.3. Расчет симметричных систем общего вида
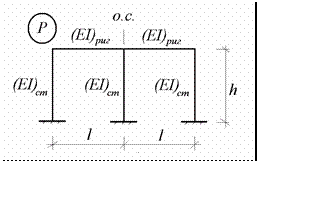Рассмотрим одноэтажную двух пролетную раму (8.7)
Рис.8.7
удовлетворяющую все признакам симметрии и обладающую осью симмет- рии. На раму действует произвольная нагрузка, показанная на рис.8.7 ус- ловным буквенным обозначением P.
Рассматриваемая рама шесть раз статически неопределимая система
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.