Метод сил, страница 8

Исключая  из каждого соотношения (8.24) с помощью (8.21) первые n+1 слагаемое, получим величины абсолютных ошибок, связанные с реше- нием канонических уравнений

11   1                        1n    n              1             1

± d  e  ± ... ± d  e   = D  - D  ¹ 0

+            .................................................

n1   1                        nn    n               n             n

± d  e  ± ... ± d  e   = D  - D  ¹ 0

+             -

Для оценки допустимости погрешностей найденных значений основных неизвестных  вычисляются  относительные  ошибки,  возникающие  при  ре- шении канонических уравнений. При этом возможны два исхода.

При первом исходе величина относительной ошибки в каждом каноническом уравнении не превышает 5%

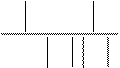D+  - D

+         -

1            1           £ 5%

min( D1  , D1  )

...............

D

n

n

+   - D-

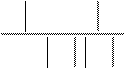
£ 5%

min( D+   , D-   )

n    n

+         -

Здесь

min( Di  , Di  )

(i = 1,..., n)

означает,  что  из  двух  величин  берется  наи-

меньшая по модулю. В этом случае считается, что канонические уравнения решены правильно и основные неизвестные найдены с достаточной точно- стью.

При втором исходе величины относительных ошибок в отдельных или во всех канонических уравнениях превышают 5%

D

k

k

+   - D+          -

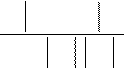
> 5%

(k = 1,..., m; 1 £ m £ n)

min( Dk  , Dk  )

В этом случае считается, что канонические уравнения решены неправильно, а основные неизвестные найдены с недостаточной точностью.

8.2.2. Окончательные поверки метода сил

1.Статическиеокончательныеповерки– осуществляются в задан- ной  системе  после  построения  эпюр  окончательных  внутренних  усилий. Они заключаются в проверке равновесия узлов, стержней и заданной сис- темы  в  целом  по  тем  же  правилам,  что  и  для  статически  определимых стержневых систем.

Такие  поверки  позволяют  проверить  правильность  получения  окон- чательных  эпюр  при  умножении  единичных  эпюр  внутренних  усилий  на основные неизвестные и сложении их между собой и с грузовыми эпюра- ми. Но они не позволяют проверить правильность составления канониче- ских уравнений и нахождения основных неизвестных.

2.Кинематическиеокончательныеповерки–  осуществляются  в заданной системе после построения эпюр окончательных внутренних усилий. Они заключаются в последовательном умножении каждой единичной

эпюры  изгибающих  моментов моментов и имеют вид:

mi на  эпюру  окончательных  изгибающих

-   при расчете на действие нагрузки

m M

å ò   i        P ds = 0

( i = 1,...,n )

k     s      EI

-   при расчете на действие температуры

mi M t ds = -D

( i = 1,...,n )

ò

å                 it

k     s      EI

-   при расчете на действие осадки опор

mi M S ds = -D

( i = 1,...,n )

ò

å                 is

k     s       EI

Такие  поверки  позволяют  проверить  правильность  составления  ка- нонических  уравнений  и  нахождения  основных  неизвестных.  Но  они  не позволяют  проверить  правильность  исходных  эпюр  внутренних  усилий  в единичных состояниях и грузовом состоянии.

Таким образом, две окончательные поверки взаимно дополняют друг друга  и  только  в  случае  выполнения  каждой  из  них  можно  полагать,  что внутренние усилия в заданной системе от действующих внешних факторов найдены правильно.

8.3. Особенности расчета методом сил симметричных плоских статически неопределимых стержневых конструкций

8.3.1. Возможные упрощения составления и решения канонических уравнений метода сил

Центральным  моментом  расчета  статически  неопределимых  стерж- невых конструкций методом сил является составление канонических урав- нений  и  их  решение  для  определения  основных  неизвестных.  Поэтому трудоемкость расчета, прежде всего, зависит от числа составляемых кано- нических  уравнений.  Число  таких  уравнений  равняется  степени  статиче- ской  неопределимости  рассчитываемой  стержневой  конструкции  и  для произвольной статически неопределимой стержневой конструкции состав- ляется система n канонических уравнений

d11 X1  + ... + d1k X k  + d1k +1 X k +1  + ... + d1n X n  + D1P  = 0

..............................................................................