1)Динамическая нагрузка- нагрузка изменяющаяся во времени с конечной скоростью по величине, направлению и месту приложения
Особенности: 1)возникновение сил инерции масс нагрузок и масс сооружения;2)возникновение напряжений, внутренних усилий, деформаций, перемещений переменных во времени;3)возникновение колебательного движения конструкции
Разновидности: подвижная, неподвижная, ударная, сейсмическая, кратковременная
2)Основная задача динамики сооружений: определение закона колебательного движения при действии переменных во времени внешних воздействий и определение кинематических характеристик (скорости, ускорения, пермещения)
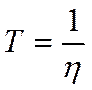
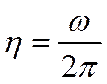 Цели: обеспечение несущей способности конструкции, безопасного уровня
воздействия колебания на людей, на производственный процесс
Цели: обеспечение несущей способности конструкции, безопасного уровня
воздействия колебания на людей, на производственный процесс
3)Частота колебаний(η)- количество колебаний в единицу времени (Гц)
Период(Т)-время за которое происходит полный цикл колебаний(сек)
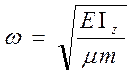
Круговая частота(ω)- (сек-1)кол-во полных колебаний за время 2П сек(![]() )
)
4)Число степеней свободы- число независимых геометрических параметров, определяющих положение колеблющейся системы с учетом деформаций материала системы. Бывает полное (без учёта допущений) и неполное (с учётом допущений).
Зависит от: количества колеблющихся масс и от числа зависимых возможных перемещений этих масс, допускаемых наложенными на них связями
5)Коэффициент жесткости(с)-способность конструкции сопротивляться деформациям. Равен величине силы которую необходимо приложить для возникновения в конструкции перемещения равного 1
Коэффициент податливости- способность конструкции поддаваться
деформациям. Равен величине перемещения, которое возникает в конструкции от
действия силы = 1 ![]()
Коэффициент динамичности-
учитывает влияние динамического характера приложения нагрузки на амплитуду
вынужденных колебаний. 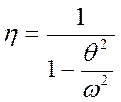
6) ![]() ;
;![]() ;
;![]()
7)Установившийся процесс- процесс при котором колебания происходят с постоянной частотой
Переходный – связан с режимом работы в период вкл/выкл(пуск/остановка)
8)Способы составления диф. ур-ий:
-Основной способ
-Прямой способ(метод перемещений)
-Обратный способ(метод сил)
9)Тривиальное решение и равенство нулю неизвестных показывают, что колебания не возникают
2)При det=0 возможно нетривиальное решение и их результатом является набор собственных частот колебаний системы
10)Спектр собственных частот – значения собственных частот ![]() , расположенных в порядке возрастания.
Находится в графической и безразмерной форме. При граф. Форме частоты
располагаются в порядке возрастания на прямой. При безразмерной первая частота делится
сама на себя, а остальные на первую.
, расположенных в порядке возрастания.
Находится в графической и безразмерной форме. При граф. Форме частоты
располагаются в порядке возрастания на прямой. При безразмерной первая частота делится
сама на себя, а остальные на первую.
Собственные формы – это очертания данной системы при найденных
значениях амплитуд. Каждому значению ![]() соответствует своя
собственная форма.
соответствует своя
собственная форма.
11)Ортогональность собственных форм – связь числа узлов с номером собственной формы состоит в том, что при их умножении произведение равно 0. Способ используется для проверки правильности вычисления
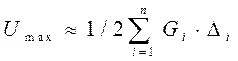 12)Энергетический метод – основан на применении закона
сохранения энергии, согласно которому сумма потенциальной и кинетической
энергии упругой системы является величиной постоянной во времени
12)Энергетический метод – основан на применении закона
сохранения энергии, согласно которому сумма потенциальной и кинетической
энергии упругой системы является величиной постоянной во времени ![]()
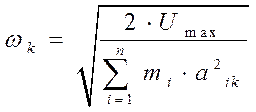
13)3 исхода при решении ур-й вынужденных колебаний. дорезонансный Qраб <![]()
![]() резонансный Qраб=
резонансный Qраб=![]() (наиболее неблагоприятно)
(наиболее неблагоприятно)
послерезонансный Qраб>![]()
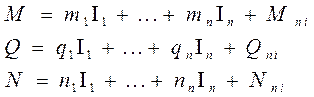 14)
14)
15) 2 исхода при решении амплитудных уравнений
Нулевые исходы и бесконечное множество исходов. Нулевые исходы означают, что система находится в покое, колебания отсутствуют. Ненулевые исходы показывают значения амплитуд (отклонение масс системы от положения равновесия)
16) при учёте сил сопротивления числовые хар-ки уменьшаются. Чем
больше силы сопротивления, тем меньше хар-ка. Характеризуются ![]()
Устойчивость есть свойство системы мало отклоняться от невозмущенного движения при малых возмущающих воздействиях
Три особенности понятия устойчивости в естествознании
1.Конкретное невозмущенное движение, устойчивость которого рассматривается
2.Вид возмущающего воздействия, по отношению к которому исследуется устойчивость невозмущенного движения
3.Интервал времени, в течение которого исследуется устойчивость невозмущенного движения
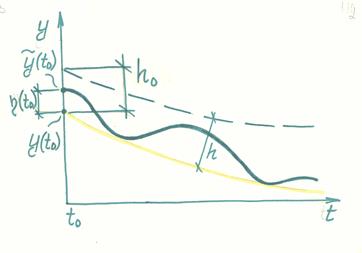
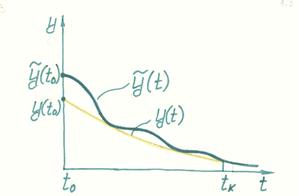 Устойчивая система по Лагранжу
Устойчивая система по Ляпунову
Устойчивая система по Лагранжу
Устойчивая система по Ляпунову
Устойчивость стержня
Прямолинейная форма равновесия сжатого стержня устойчива, если стержень будучи от нее слегка отклонен снова к ней вернется, совершая затухающие колебания
Устойчивость конструкции
Свойство конструкции сохранять свою первоначальную форму равновесия в деформированном состоянии и возвращаться к ней при малых возмущениях, совершая затухающие колебания
Потеря устойчивости
утрата конструкцией способности сохранять свою первоначальную форму равновесия при приложении к конструкции малых возмущающих воздействий
Первый тип потери устойчивости
сопровождается появлением в критическом состоянии смежных форм равновесия
Второй тип потери устойчивости
сопровождается появлением в критическом состоянии несмежных форм равновесия
Третий тип потери устойчивости
сопровождается исчезновением в критическом состоянии любых форм равновесия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.