МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
«ПОЛОЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Кафедра «Механики»
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 2
по строительной механике
«РАСЧЁТ НЕРАЗРЕЗНОЙ БАЛКИ»
Выполнил:
студентка группы 06-ПГС-5
Киналь И.В.
Проверил:
Синявская Н.В.
Новополоцк, 2009
Расчёт неразрезной балки №8
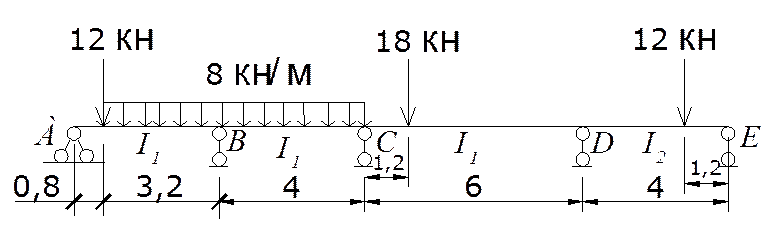
1. Кинематический анализ
1.1 Изображение расчётной схемы в виде кинематической цепи.
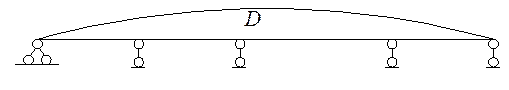
1.2 Определение числа степеней свободы
![]()
![]()
Система может быть геометрически неизменяемой и статически неопределимой.
1.3 Определение степени полной внешней и внутренней статической неопределимости.
![]() ;
;
![]() ;
;
![]() ;
;
2. Определение внутренних усилий в неразрезной балке от действия заданной постоянной нагрузки с использованием уравнения трёх моментов.
2.1. Определимся с нумерацией опор и пролётов

2.2. Образуем основную систему метода сил
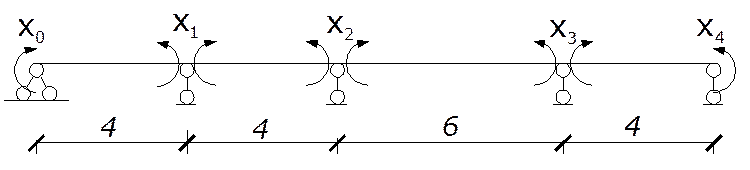
Рассмотрим основную систему метода сил на действие заданной нагрузки и построим Эпюры Мр иQp
2.3. Система уравнений трёх моментов.
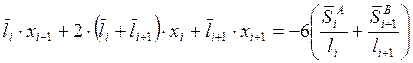
![]()
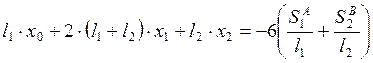
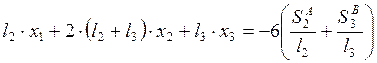
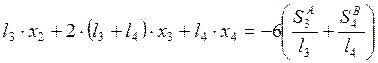
2.4. Эпюры ![]() основной системы метода сил на действие
заданной внешней нагрузки.
основной системы метода сил на действие
заданной внешней нагрузки.
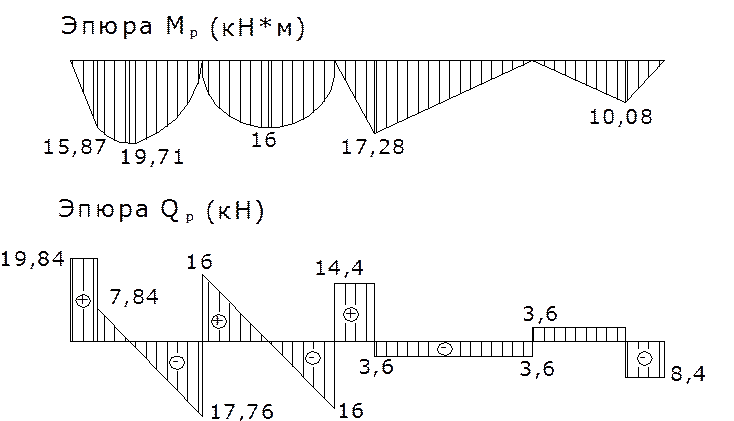
Определение величин статического
момента площадей, эпюры ![]() для каждого пролёта,
относительно вертикальных осей проходящих через опорные закрепления:
для каждого пролёта,
относительно вертикальных осей проходящих через опорные закрепления:
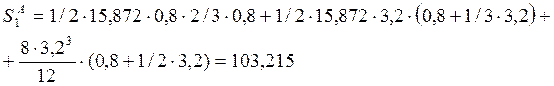
Пролёт №1:
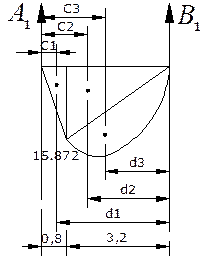
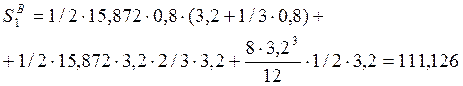
Пролёт №2:
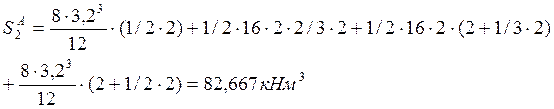
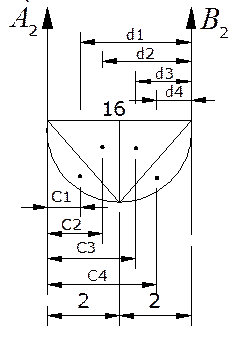
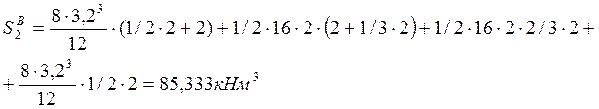
Пролёт №3:
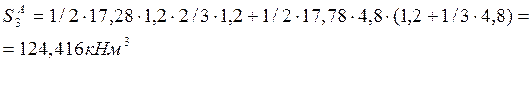
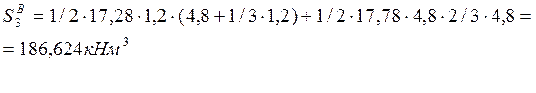
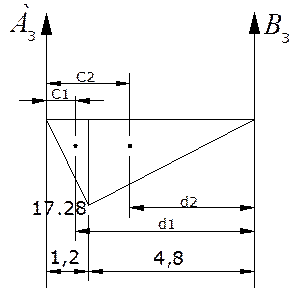
Пролёт №4:
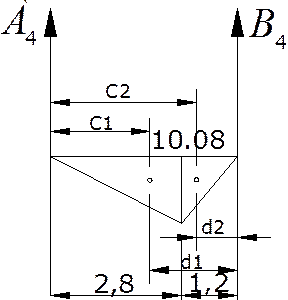
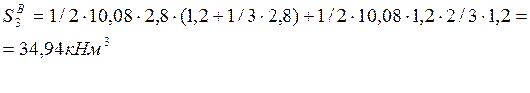
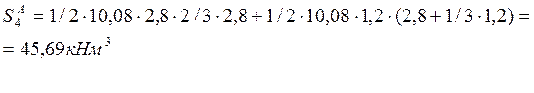
Определение значений приведённых длин и приведённых статических моментов:
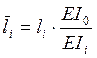
![]()
![]()
![]()
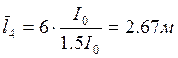
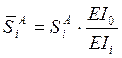
![]() ;
;![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
;
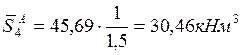 ;
; 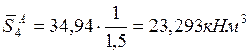
2.5. Система уравнений трёх моментов в численном виде.
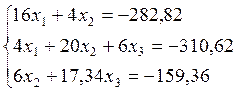
.
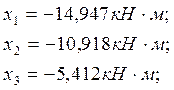
Строим эпюру опорных моментов Хоп
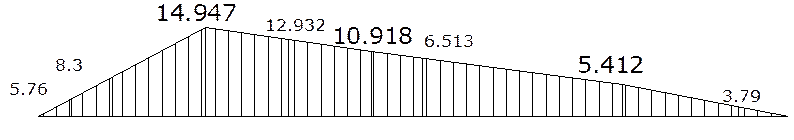
Строим окончательную эпюру изгибающих моментов
М=Мр+Хоп
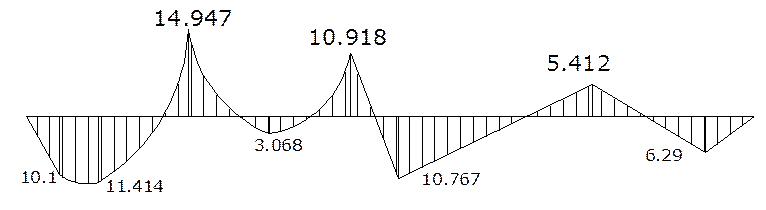
2.6. Определение величины Qпопр на каждом пролете и построение эпюры Qпопр.
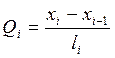
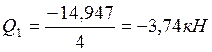
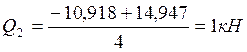
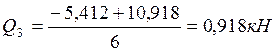
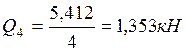
Эпюра Qпопр
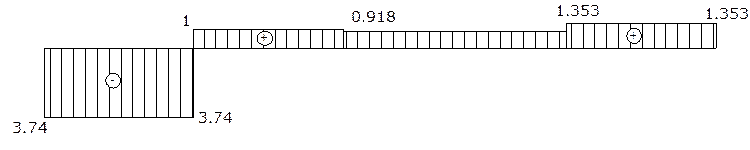
2.7. Строим окончательную эпюру поперечных сил
Q=Qp+Qпопр
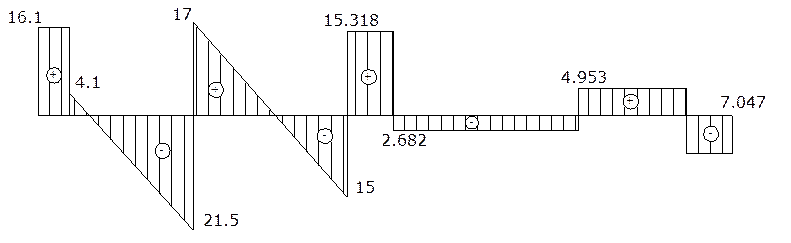
2.8. Вычисление опорных реакций.
![]()
![]()
![]()
![]()
![]()
![]()
2.10. Проверка равновесия рамы вцелом.
![]()
![]()
Равновесие балки выполнено точно
3. Расчёт неразрезной балки на заданную нагрузку методом моментных фокусных отношений.
3.1. Определение моментных фокусных отношений, используя рекуррентные формулы:
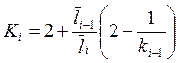 ;
;
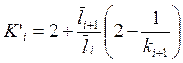 ;
;
![]()
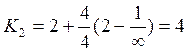
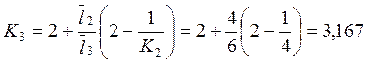 ;
;
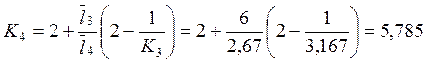 ;
;
![]()
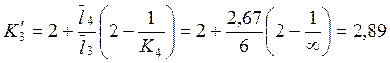
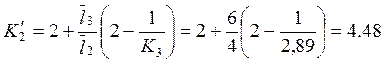
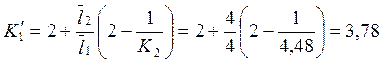
3.2. Нахождение опорных моментов от последовательного нагружения постоянной нагрузкой каждого пролёта балки.
Пролёт №1:
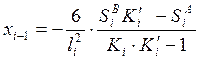
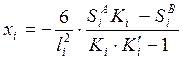
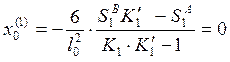
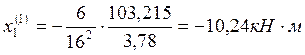
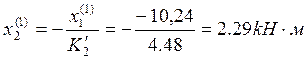
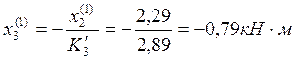
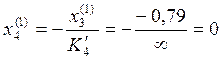
Пролёт №2:
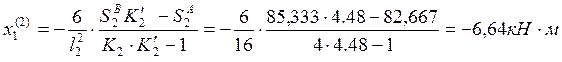
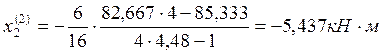
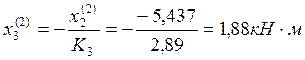
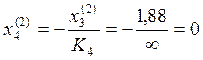
Пролёт №3:
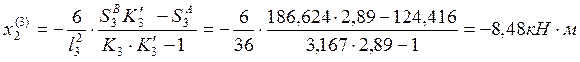
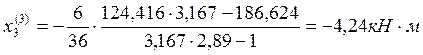
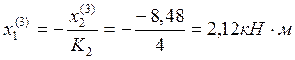
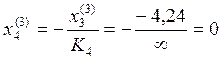
Пролёт №4:
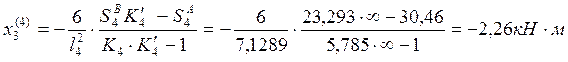
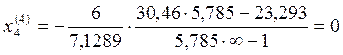
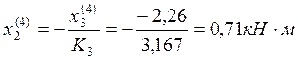
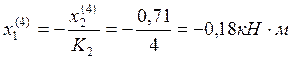
Определим опорные моменты от одновременного загружения постоянной нагрузкой всей балки
![]()
![]()
![]()
![]()
![]()
4. Расчет неразрезной балки на действие временной нагрузки
4.1 Расчет неразрезной балки на действие
временной нагрузки рассмотрим на примере построения объемлющих эпюр, на
действие в один пролёт. В качестве такого пролёта принимаем пролёт, в котором
имеется равномерно-распределённая нагрузка ![]()
4.2. Построим эпюры изгибающих моментов от загружения каждого пролёта в отдельности.
Временной нагрузкой загружаем первый пролёт:
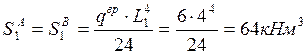
Определим опорные моменты по концам загруженного пролёта.
![]()
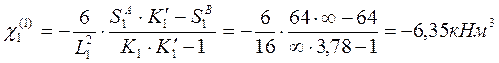
Опорные моменты по концам незагруженных пролётов
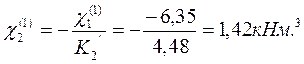
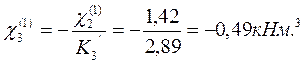
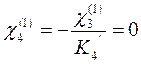
Временной нагрузкой загружаем второй пролёт:
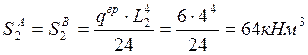
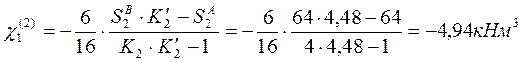
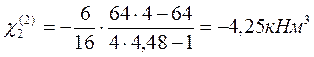
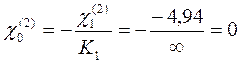
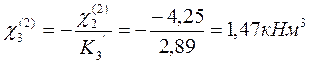
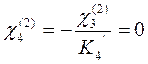
Временной нагрузкой загружаем третий пролёт:
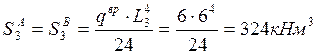
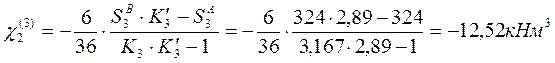
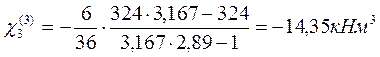
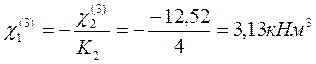
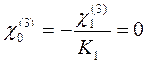
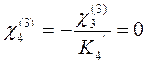
Временной нагрузкой загружаем четвертый пролёт:
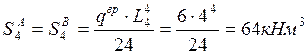
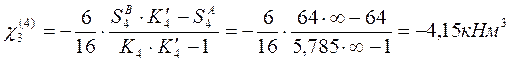
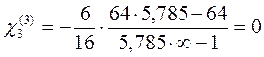
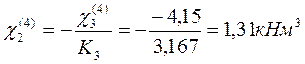
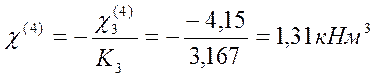
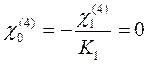
Построим эпюры Мвр от загружения временной нагрузкой каждого пролета неразрезной балки
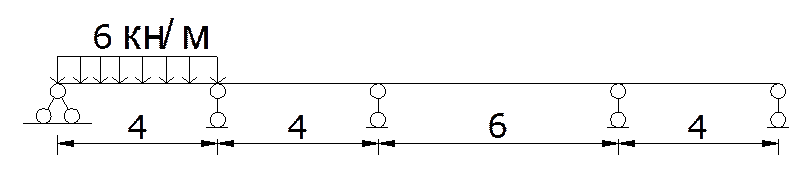
Эпюра М1вр
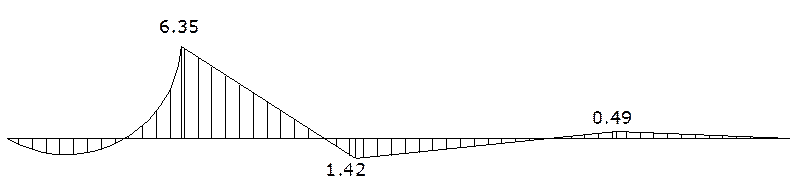
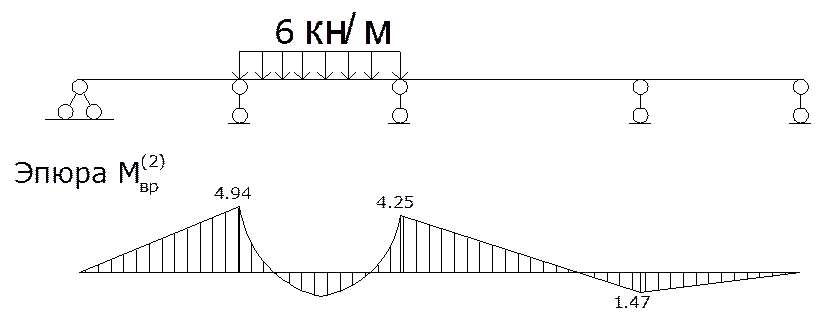
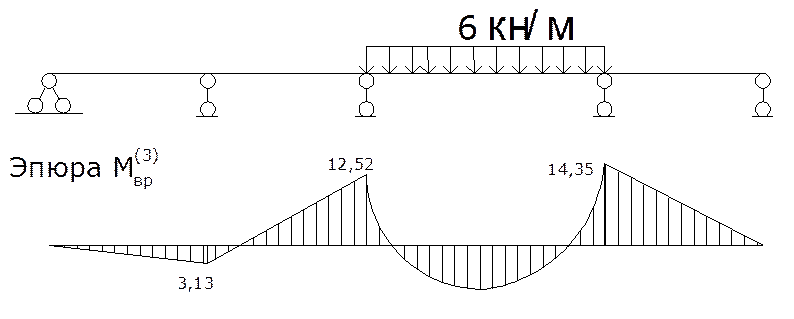
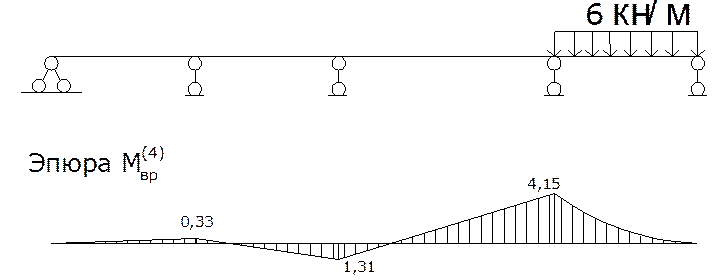
4.3. Построим объемлющую эпюру от временной нагрузки для первого пролета
Для этого разбиваем пролет на 10 равных частей и вычисляем значения ординат для всех эпюр Мвр в характерных сечениях а) Рассмотрим пролет как балку, загруженную временной нагрузкой и опорными моментами, взятыми из эпюры М1вр
б) Определяем одну из опорных реакций в) Для произвольного сечения составляем выражение для изгибающего момента г) Подставляя значения Х для каждого сечения, вычисляем значения изгибающих моментов в этих сечениях.
![]()
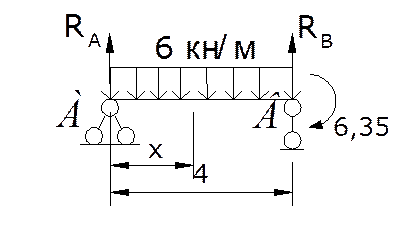
![]()
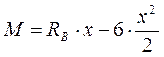
Сеч.0 х=0 М=0
Сеч.1 х=0,4 М=3,684
Сеч.2 х=0,8 М=6,408
Сеч.3 х=1,2 М=8,172
Сеч.4 х=1,6 М=8,976
Сеч.5 х=2 М=8,82
Сеч.6 х=2,4 М=7,704
Сеч.7 х=2,8 М=5,628
Сеч.8 х=3,2 М=2,592
Сеч.9 х=3,6 М= -1,401
Сеч.10 х=4 М= -6,35
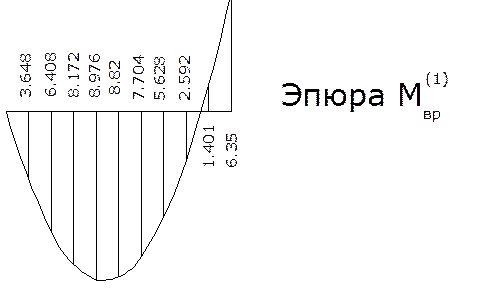
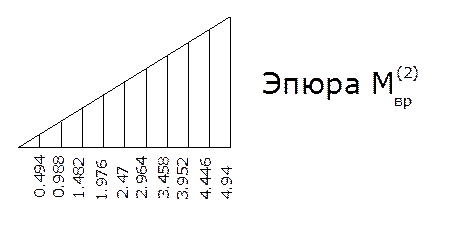
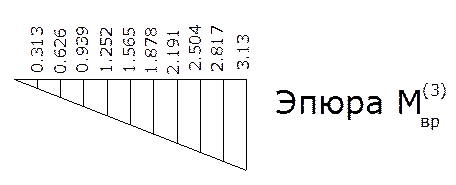
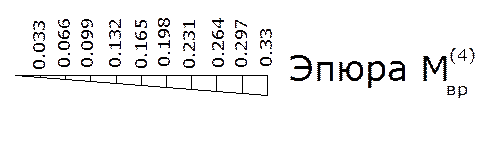
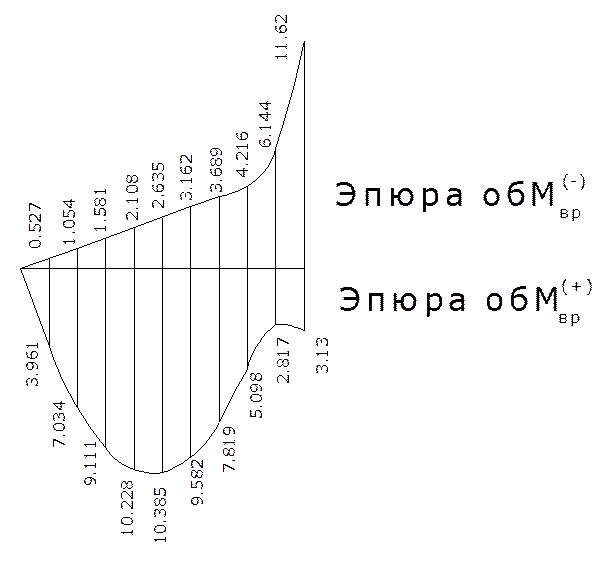
4.4. Построим объемлющие эпюры от совместного действия временной и постоянной нагрузок вместе, для этого определяем значения изгибающего момента в характерных сечениях от действия постоянной нагрузки.
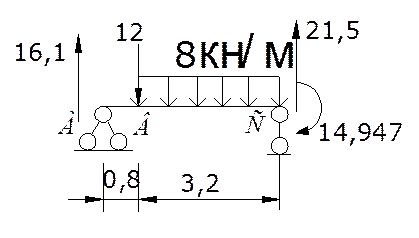
Участок ВС (0≤х≤3,2)
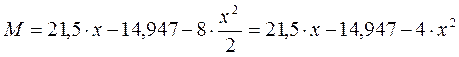
Сеч.10 х=0 М= -14,947
Сеч.9 х=0,4 М= -6,987
Сеч.8 х=0,8 М= -0,307
Сеч.7 х=1,2 М=5,093
Сеч.6 х=1,6 М=9,213
Сеч.5 х=2 М=12,053
Сеч.4 х=2,4 М=13,613
Сеч.3 х=2,8 М=13,913
Сеч.2 х=3,2 М=12,893
Участок АВ (0≤х≤0,8)
![]()
Сеч.2 х=0,8 М=12,89
Сеч.1 х=0,4 М=6,44
Сеч.0 х=0 М=0
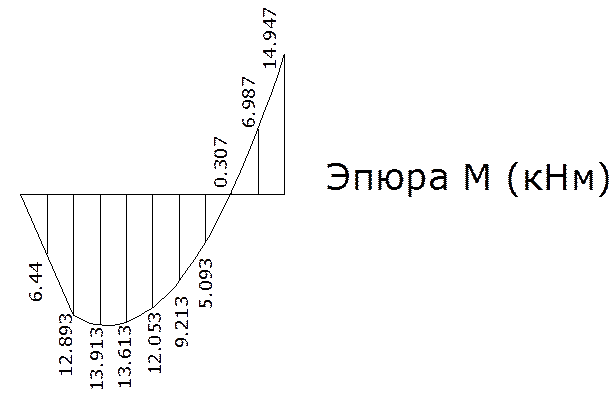
Для построения объемлющей эпюры обМмах сложим ординаты эпюры М от постоянной нагрузки с ординатами эпюры обМвр+, также и для обМmin
![]()
![]()
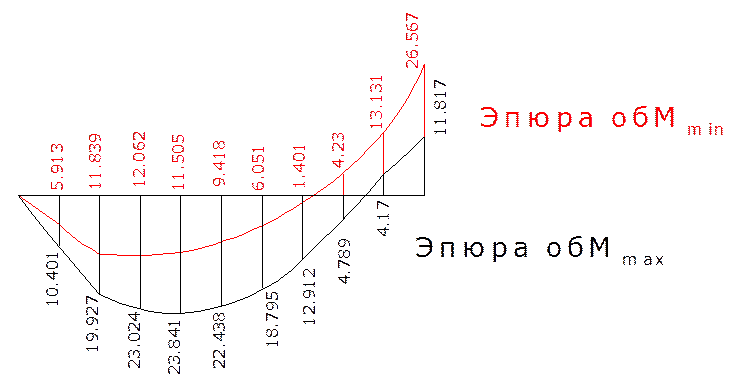
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.