Вариант 10
![]() «Расчет плоской статически определимой
рамы»
«Расчет плоской статически определимой
рамы»
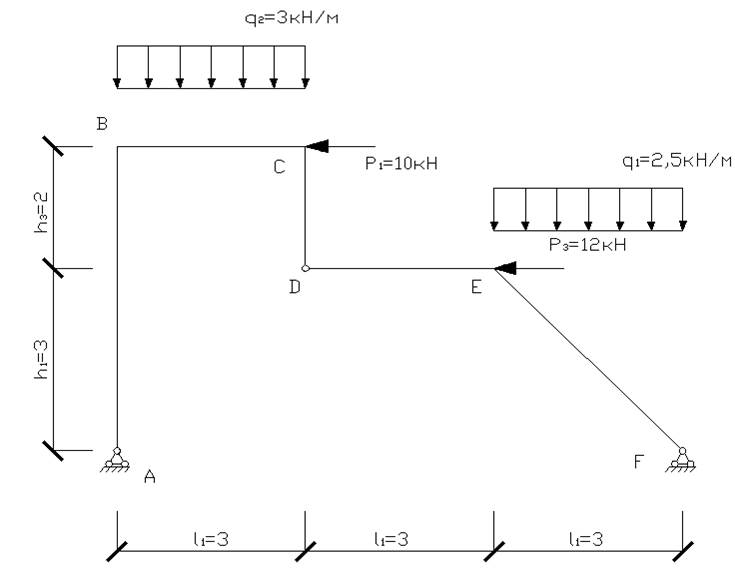
Дано: ![]() Размеры поперечного
сечения:
Размеры поперечного
сечения: ![]()
Осадка опоры А составляет 0,05м. Сечение, для которого определяется перемеение-1
Направление перемещения-вертикальное.
1.Кинематический анализ.
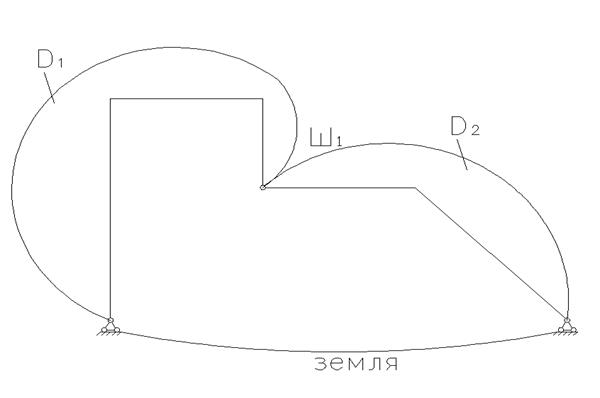
1.1 Изобразим расчетную схему плоской рамы в виде кинематической цепи.
1.2 Подсчитаем число степеней свободы.
Д=2, У=0, Ш=1, С=0, Соп=4
W=3Д+2У-2Ш-С-Соп=6+0-2-2-4=0
Следовательно, система может быть геометрически неизменяемой и статически определимой.
1.3 Выполним анализ геометрической структуры.
Диск Д1, Д2, и диск «земля» соединяются между собой
шарниром и четырьмя стержнями (эквивалентными еще двум шарнирам) , ![]() при помощи трех шарниров не лежащих на
одной прямой и образуют единый диск.
при помощи трех шарниров не лежащих на
одной прямой и образуют единый диск.
Вывод: система геометрически неизменяема и статически определимая.
2.Определение внутренних усилий в раме
от заданной постоянной нагрузки.
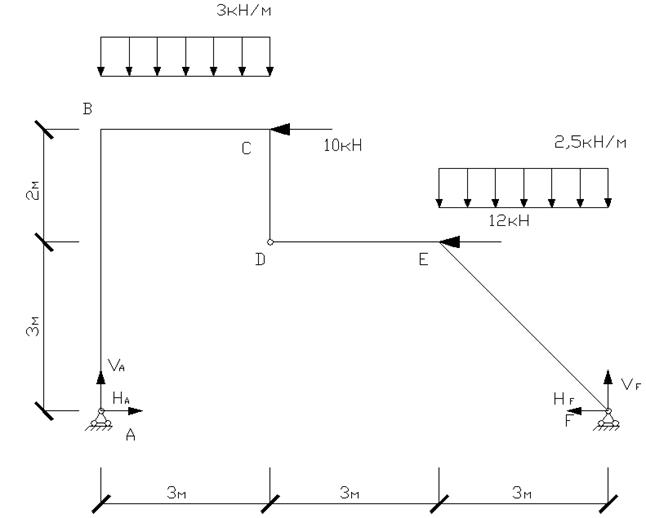 2.1 Изображаем расчетную схему рамы в
масштабе с расстановкой нагрузки и размеров в числовой форме.
2.1 Изображаем расчетную схему рамы в
масштабе с расстановкой нагрузки и размеров в числовой форме.
2.2 Определим длины наклонных элементов рамы и значения тригонометрических функций углов их наклона.
![]()
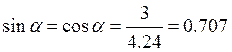 ,
, 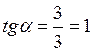
2.3 Определим величины опорных реакций в раме.
![]()
![]()
Проверка: ![]()
![]()
![]()
Проверка:![]()
Вывод: опорные реакции найдены верно.
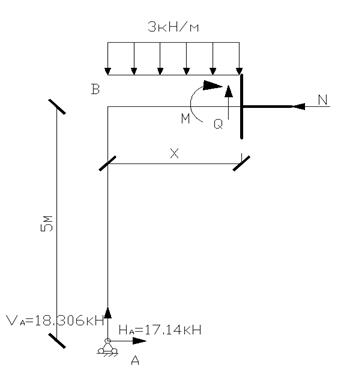
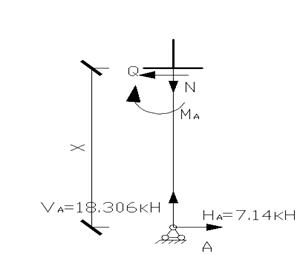 2.4 Составим аналитические выражения по
участкам рамы и определим их истинные значения для характерных сечений.
2.4 Составим аналитические выражения по
участкам рамы и определим их истинные значения для характерных сечений.
Участок АВ: (0![]() x
x![]() 5)
5)
N=-18.306кН
Q=-7.14кН
M=![]()
![]()
![]() ;
; ![]()
![]()
 Участок ВС:( 0
Участок ВС:( 0![]() x
x![]() )
)
N=-7.14кН
Q=18.306![]()
![]()
![]() ;
; ![]()
![]()
М=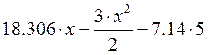
![]()
![]() ;
; ![]()
![]()
![]()
![]()
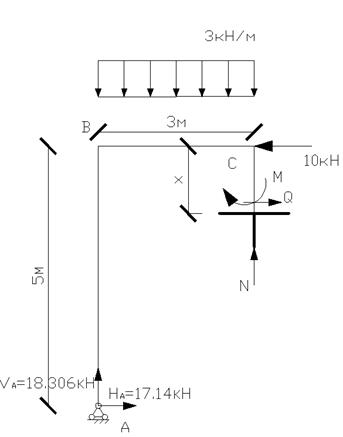
Участок СD: (0х![]() 2)
2)
N=-![]() +18.306=9.306кН
+18.306=9.306кН
Q=7.14-10=-2.86кН
М=![]()
![]()
![]() ;
; ![]()
![]()
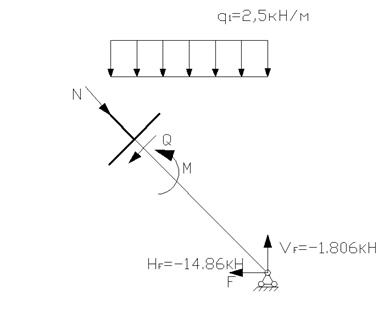 Участок FE: (0
Участок FE: (0![]() 3)
3)
N=![]()
![]() N=11.783кН;
N=11.783кН; ![]() N=17.08кН
N=17.08кН
Q=![]()
![]() Q=-9.229кН;
Q=-9.229кН; ![]() Q=-3.928кН
Q=-3.928кН
М=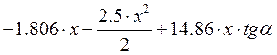
![]() М=0кНм;
М=0кНм; ![]() М=27.912кНм
М=27.912кНм
![]() М=16.708кНм
М=16.708кНм
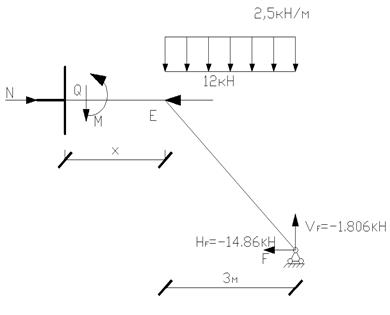 Участок ЕD: (0
Участок ЕD: (0![]() 3)
3)
N=-12+14.86=2.86кН
Q=![]() =9.306кН
=9.306кН
М=![]()
![]() М=27.912кНм;
М=27.912кНм; ![]() М=0кНм
М=0кНм
2.5 На основании расчетов аналитического метода строим эпюры М,Q,N
2.6 Выполним проверку правильности построения эпюр М,Q,N
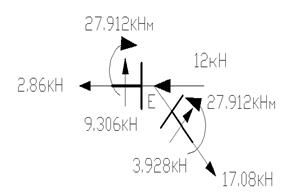 Узел Е:
Узел Е:
![]() ; 27.912-27.912=0
; 27.912-27.912=0
![]() ; -2.86-12+
; -2.86-12+![]() =0
=0
![]() ;
; ![]()
Вывод: узел Е находится в равновесии.
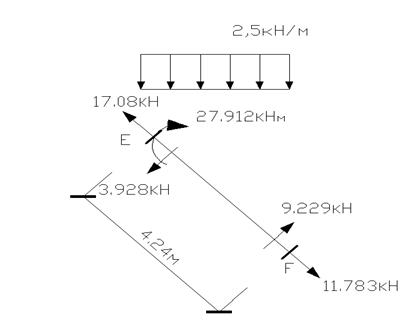 Стержень FE:
Стержень FE:
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
Вывод: стержень FE находится в равновесии.
Узел D:
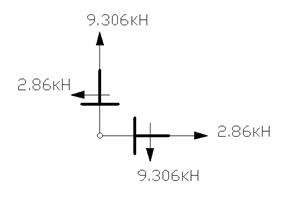
![]() ; 2.86-2.86=0
; 2.86-2.86=0
![]() ; 9.306-9.306=0
; 9.306-9.306=0
Вывод: эпюры M,Q,N построены верно.
3.Определение вертикальных перемещений сечения 1
от заданной внешней нагрузки.
3.1 Изобразим расчетную схему вспомогательного единичного состояния. Для этого в сечении 1 приложим единичную безразмерную вертикальную силу.
3.2 Определим величины опорных реакций.
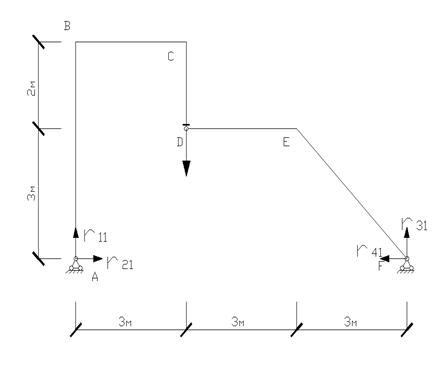
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
Проверка:
![]() ;
; ![]()
![]() ;
; ![]()
Вывод: опорные реакции определины верно.
3.3 Запишем аналитические выражения для внутренних усилий ![]() для вспомогательных участков рамы и
определим их значения для характерных сечений.
для вспомогательных участков рамы и
определим их значения для характерных сечений.
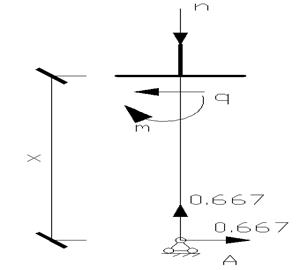
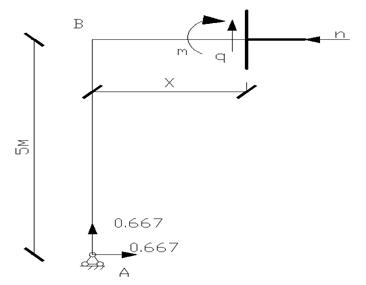 Участок АВ: (0
Участок АВ: (0![]() 5) Участок
ВС: (0
5) Участок
ВС: (0![]() 3)
3)


![]()
![]()
![]()
![]() ;
; ![]()
![]()
![]()
![]() ;
; ![]()
![]()
Участок СD: (0![]() 2)
2)
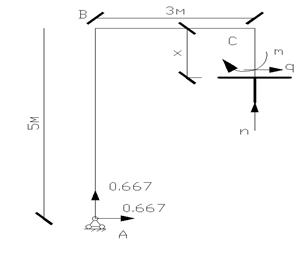
![]()
![]()
![]()
![]()
![]() ;
; ![]()
![]()
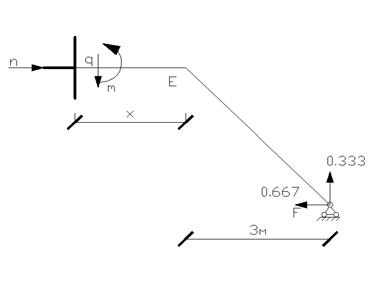
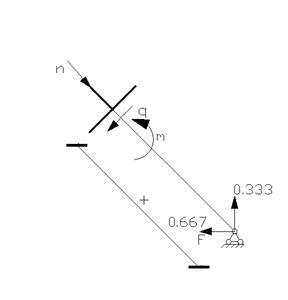 Участок EF: (0
Участок EF: (0![]() 3)
Участок FD: (0
3)
Участок FD: (0![]() 3)
3)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
; ![]()
![]()
![]()
![]() ;
; ![]()
![]()
3.4 Построим эпюры ![]() .
.
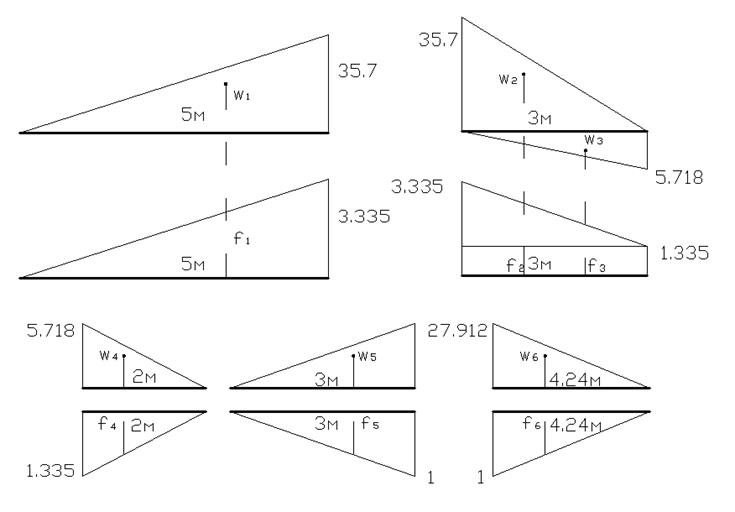 3.5 Определим перемещения по правилу
Верещагина:
3.5 Определим перемещения по правилу
Верещагина:
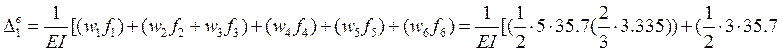
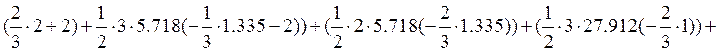
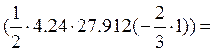
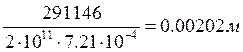
4.Определение вертикального перемещения сечения 1
от заданного температурного воздействия.
4.1 Изобразим расчетную схему рамы на заданное температурное воздействие.
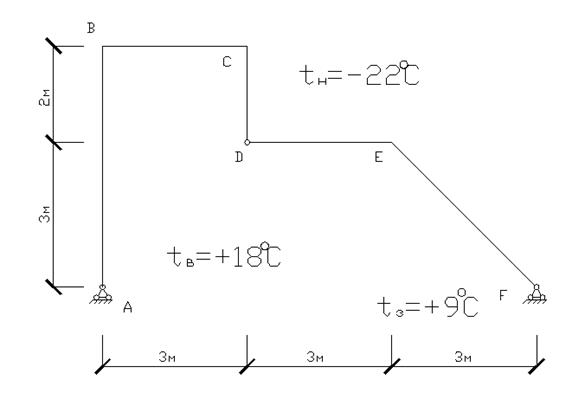 Примем:
Примем: ![]()
![]()
4.2 Определим изменение температуры во внутреннем и наружном слоях рамы.
![]()
![]()
4.3 Определим изменение температуры по оси стержней и значения удельного температурного перепада.
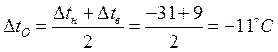
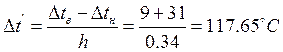
4.4 Построим эпюры изменения температуры по оси и эпюру ![]() . Эпюра
. Эпюра ![]() строится
со стороны более нагретого волокна и знаки на ней не проставляются.
строится
со стороны более нагретого волокна и знаки на ней не проставляются.
4.5 Определяем искомое вертикальное перемещение сечения 1 от заданного кинематического воздействия по формуле Мюллера-Бресслау.
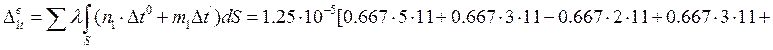
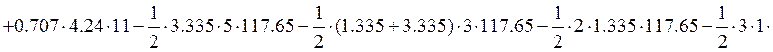
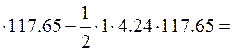
![]()
5. Определение вертикального перемещения сечения 1
от заданного кинематического воздействия.
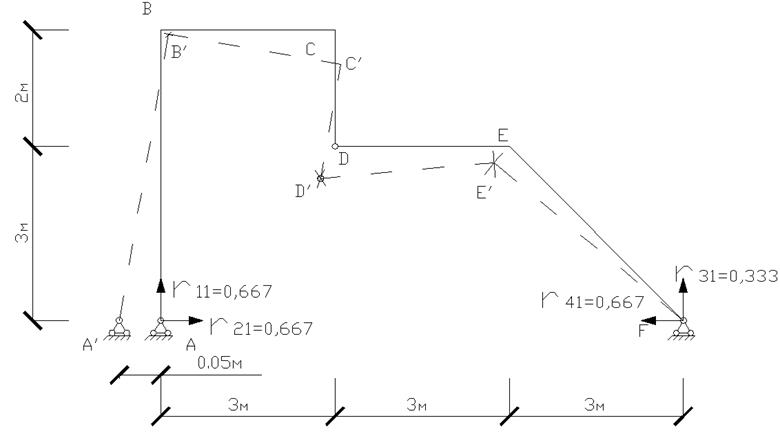 5.1 Изобразим расчетную схему рамы на
заданное кинематическое воздействие и покажем на схеме искомое перемещение.
5.1 Изобразим расчетную схему рамы на
заданное кинематическое воздействие и покажем на схеме искомое перемещение.
![]()
Шарнир D сместится вниз и влево на 0.03335 метра.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.