Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа

1. Решение алгебраических и трансцендентных уравнений

Если алгебраическое и трансцендентное уравнение достаточно сложно, то его корни редко удается найти точно. Кроме того, в некоторых случаях уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней теряет смысл. В связи с этим большое значение приобретают методы приближенного нахождения корней уравнения и оценки степени их точности.

Пусть дано уравнение

,                                                                                   (1)

где f(x) – заданная функция действительного или комплексного аргумента x.

Всякое значение с, обращающее функцию f(x)  в нуль, т.е. для которого выполняется равенство , называется корнем уравнения (1) или корнем (нулем) функции f(x).

Приближенное нахождение корней уравнения складывается из двух этапов:

1) отделение корней, т. е. нахождение наиболее узких интервалов [a, b], в каждом из которых содержится один и только один корень данного уравнения (количество интервалов определяется видом функции f(x));

2) уточнение приближенных корней, т. е. вычисление корней с заданной степенью точности.

Для отделения корней чаще всего применяют графический метод, основанный на том, что вещественные корни уравнения (1) являются точками пересечения графика функции f(x) с осью x. Следовательно, построив график , можно принять за приближенные значения корней абсциссы точек пересечения графика с осью x.

Иногда, при применении графического метода, удобно функцию f(x) представить в виде  и затем, построив графики  и , найти абсциссы их точек пересечения, которые и будут приближенными значениями корней.

Пример.

Отделить корни уравнения .

Можно построить график функции . Точки пересечения этого графика с осью x будут являться приближенными корнями уравнения.

Кроме того, можно исходное уравнение записать в виде  и построить графики  и . Абсциссы точек пересечения этих графиков можно принять за приближенные корни заданного уравнения.

Еще одним способом отделения корней является исследование функции f(x) с целью установления интервалов, на которых происходит изменение знака функции. При этом очень полезна следующая теорема:

Пусть функция f(x) непрерывна на интервале [a, b] и принимает на концах данного интервала значения разных знаков, т. е. <0. Тогда внутри интервала [a, b] найдется такая точка с, значение функции в которой равно нулю, т.е.  и которая является корнем данного уравнения.

Корень с заведомо будет единственным на [a, b], если производная  существует и сохраняет постоянный знак внутри данного интервала, т.е. если >0 или <0.

Следует отметить, что численные методы, используемые для уточнения приближенных корней, применяются для каждого найденного интервала заданного уравнения.

Рассмотрим некоторые из методов отыскания действительных корней уравнения, в основе которых лежит идея последовательного уточнения начального приближения к корню.

Метод половинного деления (метод «вилки», метод дихотомии)

Пусть дано уравнение .

Вначале определяем, какие корни требуется найти, например, только положительные или только отрицательные и т. д. Затем графическим методом находим интервалы, в каждом из которых находится только один корень данного уравнения.

Пусть искомый корень с принадлежит интервалу [a, b]. Функция  непрерывна на [a, b] и выполняется условие <0. Разделим отрезок  [a, b] пополам точкой 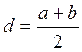 и получим уже два интервала: [a, d] и [d, b].  Далее выбираем тот отрезок, на концах которого функция f(x) принимает значения разных знаков (это значит, что внутри данного отрезка содержится корень уравнения) и опять делим его пополам. Повторяем все эти действия до тех пор, пока длина отрезка, содержащего корень, не станет меньше погрешности, с которой ищется корень.

Пример.

Методом половинного деления найти корень уравнения .

Графически находим интервал [0,4; 0,5], в котором находится действительный корень данного уравнения.

f(0,4) = -0,136 < 0;

f(0,5) =  0,125 > 0;

Условие нахождения корня в рассматриваемом интервале выполняется, т. е.

< 0.

Интервал [0,4; 0,5] делим пополам точкой 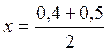 = 0,45.

Получаем два интервала: [0,4; 0,45] и [0,45; 0,5].

Для того, чтобы определить, в каком из полученных интервалов содержится искомый корень уравнения, проверим условие < 0.

f(0,4) = -0,136 < 0;

f(0,5) =  0,125 > 0;

f(0,45) = -0,00888 < 0.

< 0, следовательно, выбираем [0,45; 0,5]. Этот интервал делим пополам:

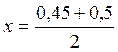 = 0,475.

Опять получаем два интервала: [0,45; 0,475] и [0,475; 0,5].

f(0,475) =  0,05717 > 0.

Т. к. < 0, то выбираем [0,45; 0,475].

Так продолжаем до тех пор, пока не найдем корень данного уравнения....

[0,453397; 0,4534];

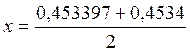 = 0,453398;

f(0,453398) =  0,0000009.

Очевидно, что  = 0,453398 является искомым корнем данного уравнения.

Метод Ньютона (метод касательных)

Метод Ньютона является весьма эффективным методом для решения алгебраических и трансцендентных уравнений. Его основное достоинство состоит в том, что при сравнительно простой схеме вычислений он обладает быстрой сходимостью. Метод Ньютона универсален и пригоден для решения обширного класса уравнений.