Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 2

Пусть корень с уравнения  принадлежит отрезку [a, b], причем,  и  непрерывны и сохраняют определенные знаки на данном отрезке.

Метод имеет простой геометрический смысл. Если - некоторое приближение к корню с уравнения, то за новое приближение x₁ принимают точку пересечения касательной, проведенной в точке  к графику функции f(x), с осью Ox.

Алгоритм поиска корня задает итерационная формула, позволяющая каждое последующее  приближение к корню вычислить через предыдущее,

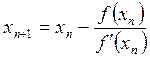, n = 0, 1, 2,...                                                           (2)

Если начальное приближение выбрано неудачно, то может случиться так, что следующее приближение x₁ к корню уравнения окажется вне интервала [a, b], что указывает на необходимость выбора другого начального приближения. В противном случае метод Ньютона может сходиться очень медленно, что приведет к накоплению погрешности вычисления, или не сходиться вообще.

Поэтому, применяя метод Ньютона, следует руководствоваться следующим правилом при выборе начальной точки : в качестве начального приближения  выбирается тот конец интервала [a, b], которому отвечает ордината того же знака, что и знак , т. е. должно выполняться условие >0 (на концах интервала).

Если >0, то принимаем = а, если >0, то = b.

Замечание. Недостатком метода Ньютона является необходимость вычисления производной для каждого . Если значение  близко к нулю, то новое приближение  может быть худшим приближением, чем . Чтобы этого избежать, иногда целесообразно применять модифицированный метод Ньютона, в котором последовательные приближения определяются формулой 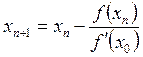. Данная формула весьма полезна, если  сложна. С другой стороны, модифицированный метод сходится значительно медленнее, чем основной метод Ньютона.

Пример.

Методом Ньютона (касательных) вычислить корни уравнения .

Графически находим, что данное уравнение имеет два действительных корня, принадлежащих интервалам [-1,4; -1,3] и [0,5; 0,6].

Сразу найдем корень, принадлежащий [-1,4; -1,3].

f(-1,4) =  0,20660 > 0,

f(-1,3) = -0,03747 < 0.

< 0, следовательно, корень находится в этом интервале.

Корень будем уточнять по формуле .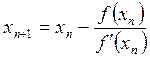

За начальное приближение принимаем тот конец интервала [-1,4; -1,3], для которого выполняется условие > 0.

,

.

 = 2,27253 > 0,

 = 2,24660 > 0.

Для точки  = -1,4 выполняется условие > 0, поэтому положим  = -1,4.

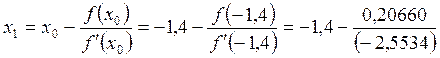 = -1,31909,

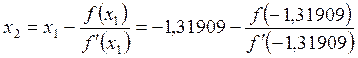 = -1,31598,

 = -1,31597,

 = -1,31597.

Один корень уравнения  = -1,31597.

Все в том же порядке повторим для интервала [0,5; 0,6].

f(0,5) = -0,10128 < 0,

f(0,6) =  0,18212 > 0.

< 0, следовательно, корень находится в этом интервале.

Для уточнения корня опять воспользуемся формулой .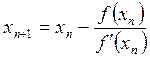

За начальное приближение принимаем тот конец интервала [0,5; 0,6], для которого выполняется условие > 0.

,

.

 = 3,64872 > 0,

 = 3,82212 > 0.

Так как для точки  = 0,6 выполняется условие > 0, то положим  = 0,6.

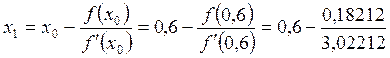 = 0,53974,

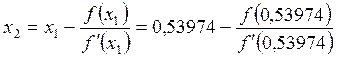 = 0,53728,

 = 0,53727,

 = 0,53727.

Другой действительный корень уравнения  = 0,53727.

Метод хорд (метод пропорциональных частей)

Пусть корень с уравнения  принадлежит отрезку [a, b], причем производные  и  непрерывны и сохраняют определенные знаки на данном отрезке. Сначала изучается расположение корней и осуществляется отделение корней. Затем выбирается начальное приближение x₀.

Правильный выбор начального приближения x₀ влияет на сходимость метода. При неправильном выборе x₀ каждое следующее приближение может все дальше удаляться от корня уравнения, т.е. метод хорд будет расходиться. Поэтому важным является следующее правило выбора начального приближения: неподвижен тот конец интервала [a, b], для которого знак функции f(x) совпадает со знаком ее второй производной , т. е. должно выполняться условие >0.

Если >0, то точка а является неподвижной, а в качестве начального приближения выбираем точку b, т. е.  и формула, определяющая алгоритм вычислений, имеет вид

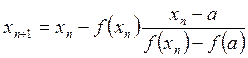.                                                         (3)

Если >0, то точка b является неподвижной, и в качестве начального приближения выбираем точку а, т. е.  и формула имеет вид