Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 15

Пример.

Методом редукции к задаче Коши найти решение краевой задачи

                                                                   

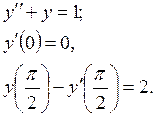
на интервале [0, ].

Решение будем искать в виде ,

где  – решение однородного уравнения ,  - частное решение неоднородного уравнения .

Сравнивая граничные условия, заданные в задаче, с краевыми условиями (39), получим:

A = 0, B = 2, .

Воспользовавшись условием (46), распишем задачу Коши для уравнения :

Примем , тогда

.                                                                   (50)

Так как , то, используя условия (48), можем записать задачу Коши для неоднородного уравнения :

.                                                                  (51)

Таким образом, исходная краевая задача для дифференциального уравнения второго порядка  распалась на две задачи Коши: (50) и (51).

Решение задачи (50) найдем, применяя метод Эйлера.

Так как метод Эйлера применяется для решения дифференциальных уравнений (и систем уравнений) первого порядка, то для понижения порядка уравнения  сделаем замену:

и тогда уравнение преобразуется в систему:

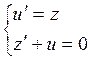 или .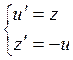

Согласно методу Эйлера, решения будем искать в виде

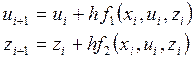 (i = 0, 1, 2,…, n),                                           (52)

где , .

Интервал [0, ] разобьем на n = 10 точек и шаг разбиения .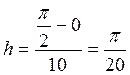

Применяя формулы (16), получим решения системы:

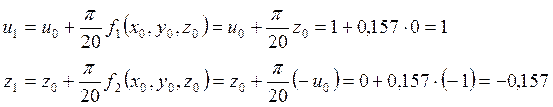
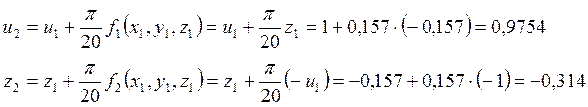
u₃ = 0,261, z₃ = -0,4672; u₄ = 0,8527, z₄ = -0,6126; u₅ = 0,7565, z₅ = -0,7465;

u₆ = 0,6393, z₆ = -0,8653; u₇ = 0,5034, z₇ = -0,9657; u₈ = 0,3518, z₈ = -1,0447;

u₉ = 0,1878, z₉ = -1,0999; u₁₀ = 0,0151, z₁₀ = -1,1295.

Задачу Коши (51) решим, применяя метод Эйлера. Для понижения порядка уравнения  сделаем замену  и получим систему:

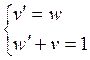или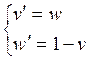

Решения будем искать в виде

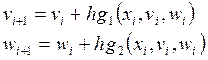 (i = 0, 1, 2,…, n),                                        (53)

где , .

Тогда

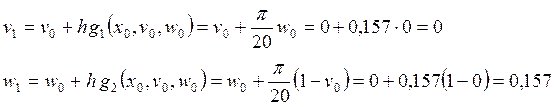
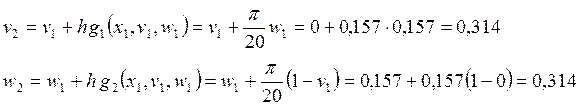
v₃ = 0,3633, w₃ = 0,4217; v₄ = 0,4295, w₄ = 0,5217; v₅ = 0,5114, w₅ = 0,6113;

v₆ = 0,6074, w₆ = 0,6880; v₇ = 0,7154, w₇ = 0,7496; v₈ = 0,8331, w₈ = 0,7943;

v₉ = 0,9578, w₉ = 0,8205; v₁₀ = 1,0866, w₁₀ = 0,8271.

Коэффициент с определим по формуле (49):

,

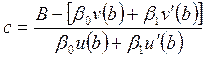где  = 0,0151,  = -1,1295,

 = 1,0866,  = 0,8271.

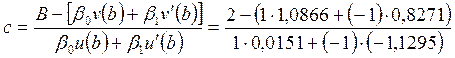 = 1,5206.

Решение исходной задачи ищем в виде .

y₃ = 1,7715; y₄ = 1,7261; y₅ = 1,6617; y₆ = 1,5795; y₇ = 1,4809; y₈ = 1,3680;

y₉ = 1,2434; y₁₀ = 1,1096.

____________________________________________________________________________

Найти решение задачи Коши:

5.6.	5.21.
5.7.	5.22.
5.8.	5.23.
5.9.	5.24.
5.10.	5.25.
7.	5.26.
5.11.	5.27.
5.12.
5.13.
5.14.
5.15.

5.28. Материальная точка массой m движется по прямой под влиянием упругой силы, стремящейся вернуть точку в положение равновесия и пропорциональной удалению точки от этого положения равновесия (k₁m –коэффициент пропорциональности). Движение происходит в среде, сопротивление которой пропорционально кубу скорости (k₂m –коэффициент пропорциональности). Составить математическую модель движения, если в момент времени t = 0 удаление и скорость равны единице. Найти численное решение задачи Коши на [0; 0,2], если k₁ = 1, k₂ = 0,1.

5.29.Материальная точка единичной массы брошена вертикально вверх с начальной скоростью u₀. Сила сопротивления среды при единичных значениях коэффициентов определяется по формуле , где x – высота подъема в момент времени t. Составить математическую модель движения точки, если в момент t = 0 высота подъема равнялась нулю. Найти численное решение задачи Коши на [0,1] при u₀ = 10 м/с.

6. Метод сеток решения уравнений параболического типа

В качестве примера применения метода сеток  для решения уравнений параболического типа рассмотрим решение смешанной задачи для уравнения теплопроводности.

Пусть дано уравнение теплопроводности

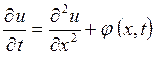.                                                                   (1)

Требуется найти функцию , которая в области  удовлетворяет уравнению (1) с условием на прямой

,                                                               (2)