а на границе области D при x = 0 и x = 1 условиям
![]() , (3)
, (3)
![]() . (4)
. (4)
Функции ![]() считаются известными.
считаются известными.
Считаем, что
задача (1)-(4) имеет единственное решение ![]() ,
непрерывное в области D вместе со своими
частными производными
,
непрерывное в области D вместе со своими
частными производными 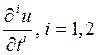 , и
, и 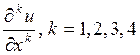 .
.
Выберем
прямоугольную равномерную сетку и заменим область D,
в которой поставлена задача (1)-(4), сеточной областью ![]() .
Область
.
Область ![]() представляет собой совокупность точек
(узлов)
представляет собой совокупность точек
(узлов) ![]() , координаты которых определяются по
правилу
, координаты которых определяются по
правилу
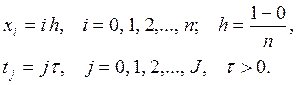 (5)
(5)
Узлы, лежащие на прямых x = 0, x = 1 и t = 0, t = T, считаются граничными узлами, все остальные – внутренними.
Для замены
частных производных в уравнении (1) разностными отношениями рассмотрим
разложение функции ![]() в ряд Тейлора:
в ряд Тейлора:
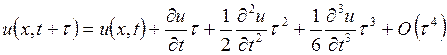 (6)
(6)
Отсюда
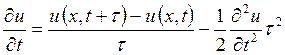 ,
,
или
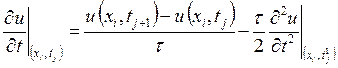 ,
, ![]() £
£![]() £
£![]() , (7)
, (7)
где 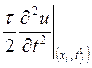 - погрешность первого порядка по
шагу
- погрешность первого порядка по
шагу![]() , т. е.
, т. е. ![]() .
.
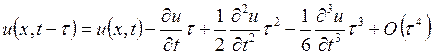 . (8)
. (8)
Таким образом
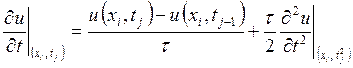 ,
, ![]() £
£![]() £
£![]() , (9)
, (9)
где 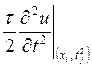 - погрешность первого порядка по
- погрешность первого порядка по ![]() , т. е.
, т. е. ![]() .
.
Чтобы получить
еще один вид аппроксимации производной ![]() конечно-разностными
соотношениями, из (6) вычтем (8):
конечно-разностными
соотношениями, из (6) вычтем (8):
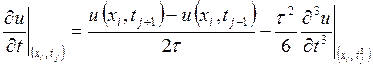 ,
, ![]() £
£![]() £
£![]() , (10)
, (10)
где 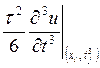 - погрешность аппроксимации второго
порядка по
- погрешность аппроксимации второго
порядка по ![]() , т. е.
, т. е. ![]() .
.
Далее разложим
функцию ![]() в ряд Тейлора
в ряд Тейлора
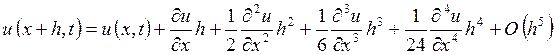 (11)
(11)
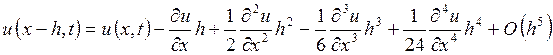 (12)
(12)
Если сложить (11) и (12), то получим разностное отношение для замены второй производной
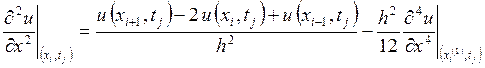 . (13)
. (13)
где 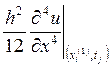 - погрешность аппроксимации второго
порядка по шагу h, т. е.
- погрешность аппроксимации второго
порядка по шагу h, т. е. ![]() .
.
Для одной и той же задачи можно составить несколько разностных схем. В качестве примера рассмотрим следующую схему:
для внутренних узлов сетки
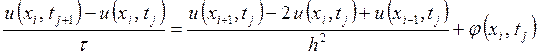 ,
,
для граничных узлов
![]() ,
,
![]() ,
, ![]() .
.
Учитывая, что в узлах сетки ![]() , получим
, получим
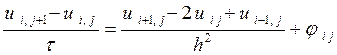 , (14)
, (14)
![]() , (15)
, (15)
![]() ,
, ![]() . (16)
. (16)
Разностная
схема (14)-(16) является устойчивой при условии 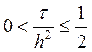 .
Погрешность аппроксимации такой схемы порядка
.
Погрешность аппроксимации такой схемы порядка ![]() .
.
При реализации разностной схемы на первый план выходит свойство устойчивости схемы. Разностную схему называют устойчивой, если вычислительная погрешность при переходе от одного слоя к другому (в процессе вычислений) не возрастает; если же вычислительная погрешность быстро растет, то схема называется неустойчивой.
Можно привести еще одну разностную схему для задачи (1):
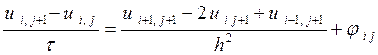 . (17)
. (17)
Пример.
Методом сеток найти решение уравнения
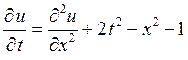 ,
,
удовлетворяющее начальным и граничным условиям
![]() ,
,
![]() .
.
Построим
сетку, выбрав шаг 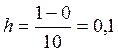 по оси x,
а по оси t:
по оси x,
а по оси t: 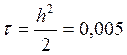 ;
; ![]() ,
,![]() .
.
Аппроксимируем данную задачу разностной схемой (14)-(16):
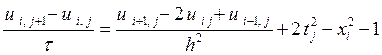
![]() ,
,
![]() ,
,
![]() .
.
Так как 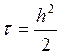 , то получим
, то получим 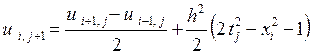 .
.
Используя
начальное условие ![]() , получим решения (значения
сеточных функций) в слое
, получим решения (значения
сеточных функций) в слое ![]() :
:
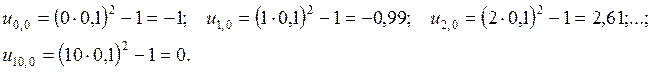
Используя краевые условия, получим:
![]() .
.
![]() .
.
Решения во внутренних узлах сетки получим из конечно-разностного уравнения
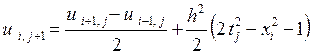 .
.
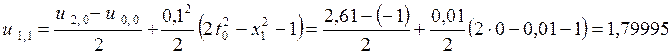 и т. д.
и т. д.
___________________________________________________________________________
6.1. Найти решение уравнения теплопроводности
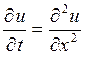 ,
,
удовлетворяющее начальным и краевым условиям
![]() ;
;
![]() .
.
6.2. Найти решение уравнения теплопроводности
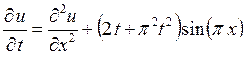 ,
,
удовлетворяющее начальным и краевым условиям
![]() ;
;
![]() .
.
Сравнить
решение уравнения теплопроводности, полученное методом сеток, с точным
решением ![]() .
.
6.3. Найти решение уравнения теплопроводности
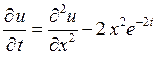 ,
,
удовлетворяющее начальным и краевым условиям
![]() ;
;
![]() .
.
6.4. Найти решение уравнения теплопроводности
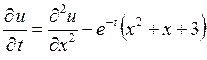 ,
,
удовлетворяющее начальным и краевым условиям
![]() ;
;
![]() .
.
6.5. Найти решение уравнения теплопроводности
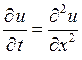 ,
,
удовлетворяющее начальным и краевым условиям
![]() ;
;
![]() .
.
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. М., 1970.
2. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М., 1972.
3. Бахвалов Н., Жидков Н., Кобельков Г. Численные методы. М., 2001.
1. Самарский А.А. Введение в численные методы. М., 1989.
2. Турчак Л.И. Основы численных методов. М.,1987.
3. Калиткин Н.Н. Численные методы. М., 1978.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.