Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 4

Оценка погрешности n-го приближения  к корню с уравнения такова:

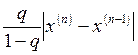£,                                                       (15)

где  на [a, b].

Замечание1. При нахождении корня уравнения  с заданной точностью >0 или при оценке погрешности n-го приближения  можно, не вычисляя точного значения числа  на [a, b], ограничиться следующей практической рекомендацией:

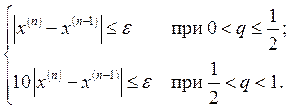£                         (16)

Замечание2. Преимущество метода итерации заключается в том, что сходимость процесса не зависит от выбора начального приближения . Отдельная ошибка, допущенная при вычислениях, не выводящая за пределы отрезка [a, b], не повлияет на конечный результат. Здесь мы встречаемся со свойством самоисправляемости сходящегося итерационного процесса.

Пример 1.

Методом итерации решить уравнение .

Графически отделяя корни данного уравнения, заключаем, что уравнение имеет единственный действительный корень, принадлежащий отрезку [1,1; 1,2].

Преобразуем данное уравнение к виду (6) следующим образом: . При таком преобразовании функция . Проверим выполнение условия сходимости (8).

.

 >1

>1.

Видно, что условие сходимости (8) не выполняется и такое преобразование не подходит, т. к. метод будет расходиться.

Пример 2.

Методом итерации найти решение уравнения

.                                                            (17)

При помощи графического метода отделим корни уравнения, т. е. найдем интервалы, в каждом из которых содержится единственный корень уравнения. Данное уравнение имеет один действительный корень, который содержится в интервале [1,6; 1,7].

Проверим условие нахождения корня в интервале :

f (1,6) = - 0,144 < 0,

f (1,7) = 0,353 > 0.

, следовательно, корень данного уравнения  действительно содержится в интервале [1,6; 1,7].

Перепишем уравнение (17) в виде , где 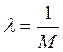, M – наибольшее значение производной  на [1,6; 1,7].

.

 = 4,88 – m,

 = 5,07 – М.

Отсюда

.

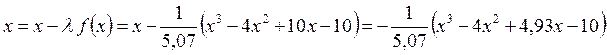Итерационная формула для нахождения корня уравнения (17) будет иметь вид

.

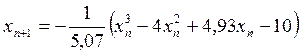В качестве начального приближения принимаем точку  = 1,6. Тогда

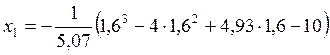 = 1,6284,

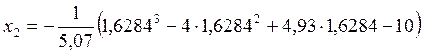 = 1,62933,

 = 1,62936,

 = 1,62936.

Следовательно, искомый корень уравнения  = 1,62936.

Рассмотрим еще один способ преобразования уравнения (17).

Преобразуем это уравнение к виду

:                                                                                   (18)

.                                                                (19)

Сравнивая (18) и (19), видим, что .

Проверим выполнение условия сходимости

£q <1,                                                                            

где q – максимальное значение производной  на интервале [1,6; 1,7].

.

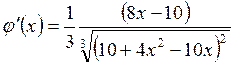  ≈ 0,356 <1,

  ≈ 0,436 <1.

Условие сходимости выполняется и корень уравнения можно уточнять, используя итерационную формулу

.

 = 1,6.

 = 1,61853,

 = 1,62528,

x₃ = 1,62781, x₄ = 1,62877, x₅ = 1,62913, x₆ = 1,62927, x₇ = 1,62932, x₈ = 1,62934, x₉ = 1,62935,

x₁₀ = 1,62935, x₁₁ = 1,62936, x₁₂ = 1,62936.

Корень уравнения x = 1,62936.

Кроме рассмотренных выше способов преобразования уравнения (17), можно предложить еще такой способ: представим исходное уравнение в виде .

Отсюда .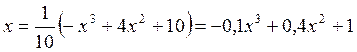

Сравнивая полученное выражение и (6), видим, что .

Проверим условие сходимости (8):

.

  = 0,512 <1,

  = 0,493 <1.

Условие сходимости выполняется и корень уравнения можно уточнять, используя формулу .

 = 1,6.

 = 1,6144,

 = 1,62175,

x₃ = 1,62550, x₄ = 1,62740, x₅ = 1,62836, x₆ = 1,62885, x₇ = 1,62910, x₈ = 1,62923, x₉ = 1,62929,

x₁₀ = 1,62932, x₁₁ = 1,62934, x₁₂ = 1,62935, x₁₃ = 1,62936, x₁₃ = 1,62936.

Корень уравнения x = 1,62936.

__________________________________________________________________________________

Численно найти корни уравнений:

                        

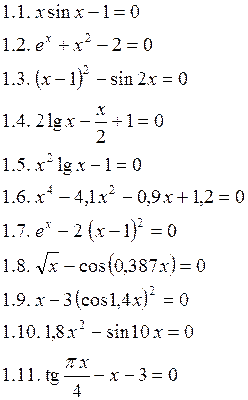
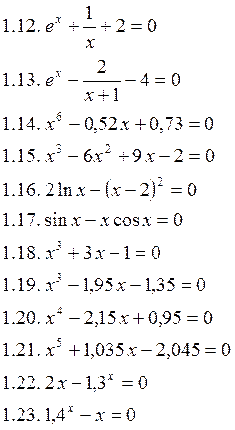
2. Решение систем линейных и нелинейных уравнений

Решение систем линейных уравнений методом итерации

Рассмотрим систему линейных уравнений

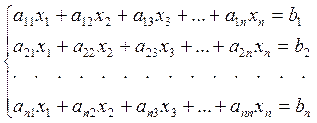                                                (1)

Решением системы (1) называется совокупность таких значений неизвестных

                                                      (2)

при котором каждое из уравнений этой системы обращается в тождество.