Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 8

Многочлен  называют многочленом наилучшего среднеквадратичного приближения функции  на [a, b]. Задача нахождения такого многочлена упрощается, если система является ортогональной на [a, b].

Функции  и  называются ортогональными на множестве точек , если скалярное произведение этих функций равно нулю, т. е. 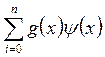 = 0 (или в другой записи  = 0).

Система функций называется ортогональной на множестве точек , если функции этой системы попарно ортогональны на этом множестве, т. е. 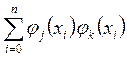 = 0,  = 0) при .

Если система  является ортогональной, то коэффициенты  обобщенного многочлена  определяются по формулам

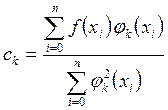.                                                                (17)

Если функция  аппроксимируется обобщенным полиномом   на отрезке [a, b], то коэффициенты  можно определить по формулам

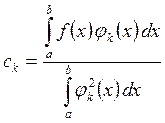.                                                                 (18)

Коэффициенты  называются коэффициентами Фурье полинома  относительно ортогональной системы функций .

Пусть на отрезке [-l, l] задана система ортогональных функций

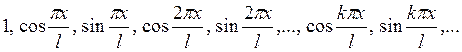                               (19)

Для  на [-l, l] тригонометрическим многочленом наилучшего среднеквадратичного приближения является тригонометрический многочлен

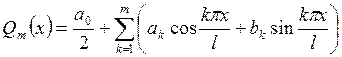,                                          (20)

где коэффициенты Фурье определяются формулами (18) и имеют вид

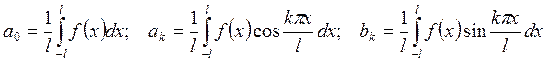, k = 1, 2,…            (21)

В качестве еще одной ортогональной системы можно рассмотреть полиномы Лежандра:

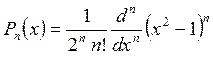 (n = 0, 1, 2,…).                                          (22)

Полиномы Лежандра образуют ортогональную систему на отрезке [-1, 1], т. е.

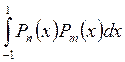 = 0 при .

Обобщенный многочлен степени n относительно ортогональной системы алгебраических полиномов Лежандра  имеет вид

,                                                  (23)

где

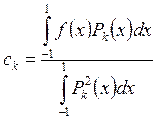.                                                                   (24)

Замечание. Если функция  определена на [a, b], то с помощью линейного преобразования

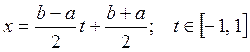                                                 (24)

можно получить полином Лежандра, ортогональный на отрезке [a, b]:

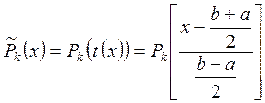.                                             (25)

Пример 1.

Найти алгебраический многочлен степени n = 2 наилучшего среднеквадратичного приближения для функции 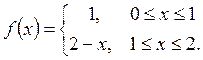 [0, 2]

Оценить погрешность.

Искомый многочлен имеет вид , где  - полиномы Лежандра (определены соотношением (25)).

Делаем замену переменных 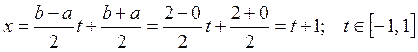 и переходим от [0, 2] к рассмотрению отрезка [-1, 1].

Получим , определенную на отрезке [-1, 1]:

.

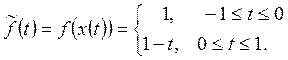Коэффициенты Фурье  найдем по формуле (24).

,

,

.

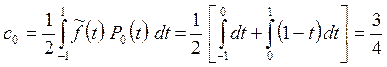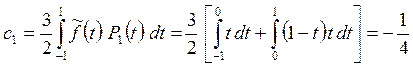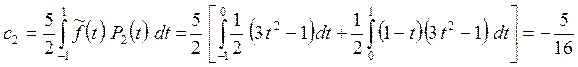Таким образом,

.

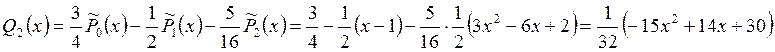Пример 2.

Имеется таблица значений:

Представить зависимость величин x и y в виде функции .

Прологарифмируем эту функцию . Если обозначить , то получим . Исходная таблица значений примет следующий вид:

Для нахождения коэффициентов а и b воспользуемся методом наименьших квадратов.

Согласно методу наименьших квадратов, сумма квадратов отклонений искомого полинома от значений  в каждой точке  должна быть минимальна, т. е.

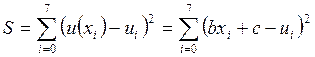- min.

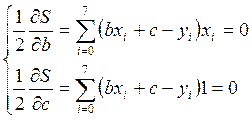
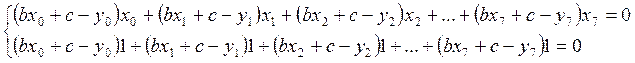
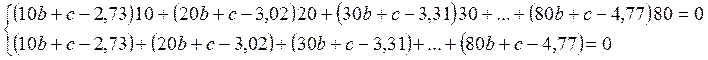
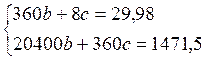
b = 0,029

c = 2,436.

= 11,472.

Тогда искомая зависимость будет иметь вид .

Интерполирование сплайнами

На практике многие кривые нельзя описать простыми функциями. Однако их можно составить из отрезков полиномов или других сравнительно простых кривых. При этом в точках стыковки полученная составная кривая будет гладкой. В теории приближения функций такие кривые называются сплайнами. Сплайн можно наглядно представить как линию, которую образует упругая линейка, закрепленная в ряде точек. Наиболее широко на практике применяются кубические сплайны.

Пусть на отрезке [a, b] задана сетка <<…<, в узлах которой заданы значения  (i = 0, 1, 2,…, n) функции , определенной на [a, b]. Причем узлы сетки <<…< не обязательно расположены равномерно. Рассмотрим задачу построения интерполяционного кубического сплайна, приближающего функцию , заданную на отрезке [a, b].