Система, имеющая решение, называется совместной, система, не имеющая решения,-несовместной. Системы называются эквивалентными, если они имеют одни и те же решения.
Систему (1) кратко можно записать в виде матричного уравнения
![]() . (3)
. (3)
Если определитель матрицы А не равен нулю (матрица неособенная), то решение системы (3) существует и единственно.
Метод итерации можно применять к решению линейной системы (1), если преобразовать ее к специальному виду. Прежде, чем проводить преобразования, необходимо проверить выполнение условий сходимости метода итерации.
Для того, чтобы метод итерации сходился, необходимо, чтобы выполнялось условие сходимости для системы (1): метод итерации сходится, если выполнены неравенства
![]() >
>![]() (i = 1, 2,
..., n), (4)
(i = 1, 2,
..., n), (4)
т. е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов, не считая свободных членов.
Преобразуем систему (1) к специальному виду: разрешим первое уравнение системы относительно x1, второе – относительно x2, третье – относительно x3 и т. д. В результате получим эквивалентную систему
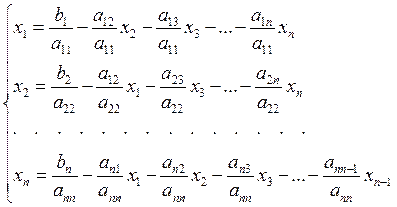 (5)
(5)
Если ввести обозначения 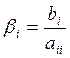 ,
, 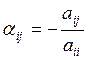 , при
, при ![]() и
и ![]() при
при ![]() (i, j = 1, 2, …., n), то
систему (5) можно представить в виде
(i, j = 1, 2, …., n), то
систему (5) можно представить в виде
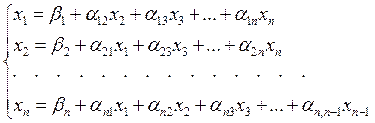 , (6)
, (6)
или в матричной форме
![]() , (7)
, (7)
где матрица a
- это матрица с нулевыми диагональными элементами. В качестве начального
приближения 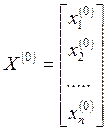 можно принять столбец свободных
членов
можно принять столбец свободных
членов 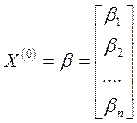 (хотя это не является обязательным
условием). Матрицу
(хотя это не является обязательным
условием). Матрицу ![]() подставляем в правую часть
системы (6) и получим
подставляем в правую часть
системы (6) и получим ![]() . Далее
. Далее ![]() подставим
в правую часть (7), получим
подставим
в правую часть (7), получим ![]() и т. д. Таким образом,
любое (n + 1) приближение вычисляется по формуле
и т. д. Таким образом,
любое (n + 1) приближение вычисляется по формуле
![]() . (8)
. (8)
Достаточное условие сходимости процесса итерации:
если для приведенной системы (6) выполнено по меньшей мере одно из условий
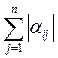 < 1 (i = 1, 2, 3, …, n) или
< 1 (i = 1, 2, 3, …, n) или
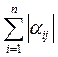 < 1 (j = 1, 2, 3, …, n), (9)
< 1 (j = 1, 2, 3, …, n), (9)
то процесс итерации (8) сходится к единственному решению этой системы, независимо от выбора начального приближения.
Замечание1. Решение
системы может быть получено с заданным числом точных десятичных знаков. Чтобы
избежать накопления погрешностей в промежуточных вычислениях, последовательные
приближения ![]() , i = 0, 1,
2,… вычисляют до совпадения всех требуемых знаков, после чего запасные знаки
округляются.
, i = 0, 1,
2,… вычисляют до совпадения всех требуемых знаков, после чего запасные знаки
округляются.
Оценка погрешности для метода итерации:
![]() ≤
≤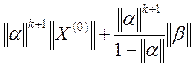 . (10)
. (10)
Пример.
Методом итерации решить систему уравнений
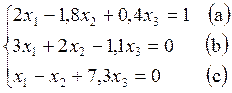
и оценить число необходимых для этого шагов.
Видно, что условие сходимости (4) для данной системы не выполняется, так как в уравнениях (а) и (b) нет диагонального преобладания. Для применения метода итерации необходимо преобразовать заданную систему к такому виду, для которого будет выполняться условие (4). Для этого умножим уравнение (а) на γ, (b) на δ, сложим оба уравнения и в полученном выражении выберем γ и δ так, чтобы имело место диагональное преобладание.
![]() .
.
Положив ![]() ,
получим
,
получим ![]() .
.
С уравнением (b) поступаем аналогично.
![]() .
.
Положив ![]() ,
получим
,
получим ![]() .
.
В результате исходная система примет следующий вид:
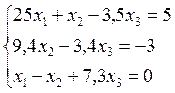 ,
,
в которой есть диагональное преобладание, т. е. для которой выполняется условие сходимости (4).
Далее, разрешив эту систему относительно диагональных неизвестных, получим так называемую приведенную систему уравнений
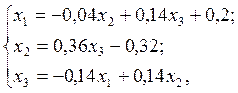
к которой можно применять метод итерации (для приведенной системы выполняется условие сходимости (9)).
В качестве начального
приближения ![]() принимаем столбец свободных членов:
принимаем столбец свободных членов:
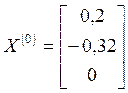 .
.
Применяя формулу (8), найдем решение системы:
![]() .
.
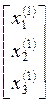 =
=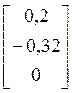 +
+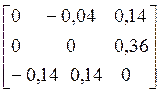
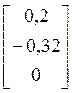 =
=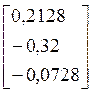 ,
,
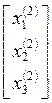 =
=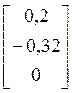 +
+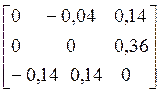
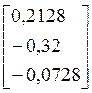 =
=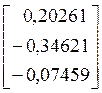 и т. д.
и т. д.
Решением исходной системы будет
матрица 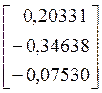 .
.
Решение систем нелинейных уравнений методом итерации
Пусть дана система нелинейных уравнений
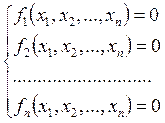 , (11)
, (11)
или в матричной форме
![]() , (12)
, (12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.