Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 12

Численное решение задачи Коши (3)-(4) состоит в том, чтобы получить искомое решение  в виде таблицы его приближенных значений для заданных значений аргумента x на некотором отрезке [a, b]: а = x₀ < x₁ < ... < x_n = b. Точки  называются узловыми точками, а множество этих точек называют сеткой на [a, b].

Выбираем малый шаг h и на отрезке [a, b] строим систему равноотстоящих точек

 (i = 0, 1, 2,…, n).                                                   (5)

Метод Эйлера заключается в том, что искомая интегральная кривая , проходящая через точку , приближенно заменяется ломаной с вершинами , звенья которой прямолинейны между прямыми  и имеют подъем

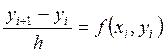.                                                                 (6)

Таким образом, каждое значение  можно найти по формуле

, (i = 0, 1, 2,…, n).                                    (7)

В результате, получим совокупность значений  численного решения задачи Коши.

В каждом узле  имеем  (i = 0, 1, 2,…, n). Причем для любого численного метода начальные условия задачи Коши выполняются точно, т. е. .

Метод Эйлера может применяться для решения обыкновенных дифференциальных уравнений высших порядков и для систем дифференциальных уравнений.

Рассмотрим систему дифференциальных уравнений первого порядка

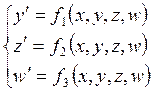
с начальными условиями .

Решения задачи Коши для данной системы уравнений можно получить, используя следующие формулы

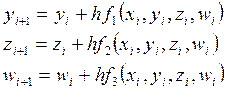 (i = 0, 1, 2,…, n).                        (8)

Дифференциальные уравнения более высокого порядка можно решить с помощью метода Эйлера путем понижения порядка уравнения (с помощью замены).

Пусть дано дифференциальное уравнение .

Делаем замену , в результате чего дифференциальное уравнение порядка m преобразуется в систему уравнений первого порядка:

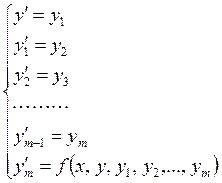
Пример.

Найти решение задачи Коши 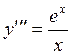, , на отрезке [1; 1,5].

Задачу решим методом Эйлера. Прежде всего, понизим порядок уравнения, сделав замену переменных , в результате чего исходное уравнение преобразуется в систему дифференциальных уравнений первого порядка:

,                                                                     

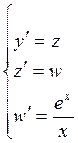с начальными условиями .

Формулы метода Эйлера, позволяющие найти решение полученной системы имеют вид:

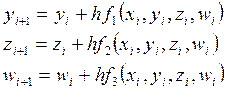 (i = 0, 1, 2,…, n),                                   

где .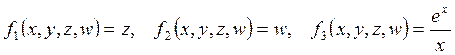

Интервал [1; 1,5] разобьем на 5 точек с шагом разбиения .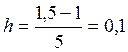

       

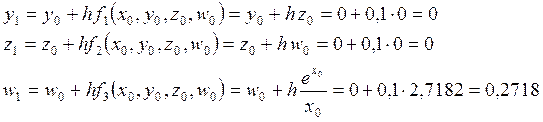
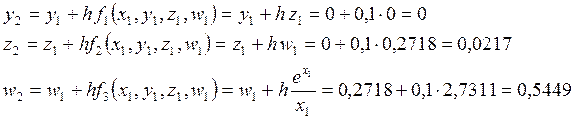
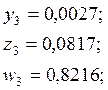
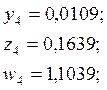
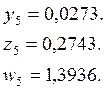
Метод Эйлера-Коши

По методу Эйлера-Коши сначала определяется «грубое» приближение решения

.                                                                 (9)

Далее вычисляем .

Затем находят более точное приближение:

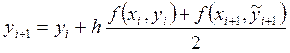.                                        (10)

Метод Эйлера-Коши еще называют методом Эйлера с пересчетом. С помощью этого метода можно проводить контроль точности решения путем сравнения значений  и  и выбора величины шага h в каждом узле в зависимости от того, насколько велико различие  и . Если величина  сравнима с погрешностями вычислений, то шаг нужно увеличить, если же эта разность слишком велика (например, >0,01), значение h следует уменьшить. Используя эти оценки, можно построить алгоритм метода Эйлера с пересчетом с автоматическим выбором шага.

Метод Эйлера можно уточнить, применяя итерационную обработку.

Вначале вычисляем

,                                                            (11)

а затем это приближение уточняется по формулам

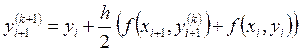.                                      (12)

Итерации продолжаем до тех пор, пока два последовательных приближения  и  не совпадут между собой в пределах требуемой точности (в соответствующих десятичных знаках). После этого  принимаем за приближенное значение .

На практике часто используются формулы приблизительной оценки точности значений численного решения методом двойного пересчета (методом Рунге). Для определения правильности выбора шага h на каждом этапе из двух шагов применяют двойной пересчет. Сначала одним из методов отыскивается значение  (i = 0, 1, 2,…, n) с шагом h, а затем проводятся вычисления с шагом . Понятно, что в последнем случае при каждом переходе от данного аргумента к следующему потребуется двукратное применение метода. Соответствующие аргументам  новые полученные значения обозначим через . Это улучшенное приближение к , и поэтому данные  (i = 0, 1, 2,…, n) возьмем в качестве искомого численного решения с шагом h.