Выразим ![]() ,
, ![]() через
значения функции
через
значения функции ![]() в узлах
в узлах ![]() ,
т. е. через значения
,
т. е. через значения ![]() .
.
Для этого воспользуемся разложением в ряд Тейлора.
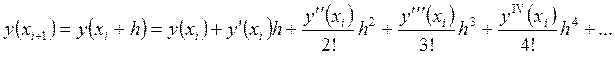 (23)
(23)
Отсюда
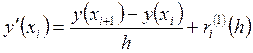 , (24)
, (24)
где 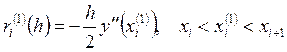 .
.
Так как
полагаем ![]() , то можем записать
, то можем записать
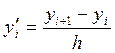 +
+ ![]() , (так
называемая правая производная) (25)
, (так
называемая правая производная) (25)
где ![]() -
погрешность первого порядка по шагу.
-
погрешность первого порядка по шагу.
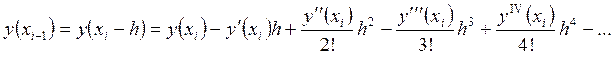 (26)
(26)
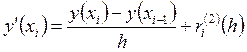 , (27)
, (27)
где 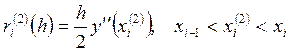 .
.
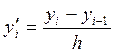 +
+ ![]() ( левая производная). (28)
( левая производная). (28)
Из (23) вычтем (26) и после небольших преобразований получим
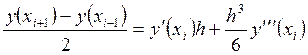 .
.
Отсюда
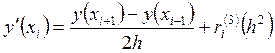 , (29)
, (29)
где 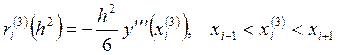 .
.
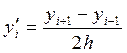 +
+ ![]() (центральная
производная). (30)
(центральная
производная). (30)
Сложив (23) и
(26), получим симметричное выражение для ![]()
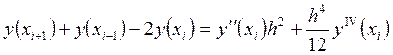 .
.
Отсюда
выражение для ![]() будет иметь вид
будет иметь вид
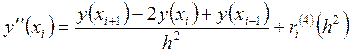 , (31)
, (31)
где 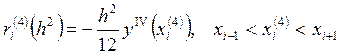 .
.
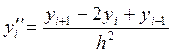 +
+
![]() . (32)
. (32)
Это не
единственно возможные выражения для ![]() и
и ![]() . Исследуя значения
. Исследуя значения ![]() в
других точках, кроме рассмотренных
в
других точках, кроме рассмотренных ![]() , можно получить другие
выражения для производных, но они будут и более сложными.
, можно получить другие
выражения для производных, но они будут и более сложными.
Заменив в
уравнении (20) производные ![]() и
и![]() выражениями (30) и (32), получим
выражениями (30) и (32), получим
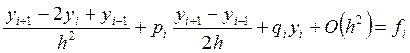 . (33)
. (33)
Таким же
образом заменяем производные ![]() и
и ![]() в граничных условиях (21).
в граничных условиях (21).
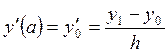 ,
, 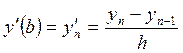 .
Такие замены производных в граничных точках имеют погрешность порядка
.
Такие замены производных в граничных точках имеют погрешность порядка ![]() .
.
Можно получить
более точные формулы для аппроксимации (замены) производных в граничных точках.
Для этого рассмотрим разложение в ряд Тейлора ![]() и
и ![]() .
.
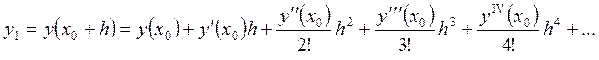 (34)
(34)
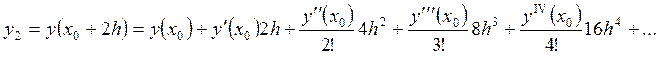 (35)
(35)
Далее (34)
умножим на 4 и из ![]() вычтем
вычтем ![]() .
После небольших преобразований получим
.
После небольших преобразований получим
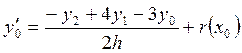 , (36)
, (36)
где 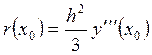 .
.
Аналогично
получим выражение для ![]() :
:
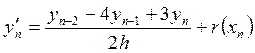 , (37)
, (37)
где 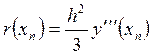 .
.
Выражения (36)
и (37) имеют погрешность второго порядка по шагу, т.е.![]() .
.
Рассмотрим на отрезке [a, b] граничную задачу для дифференциального уравнения
![]() (38)
(38)
с условиями
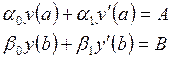 , (39)
, (39)
где p(x), q(x), f(x) непрерывны на отрезке [a, b].
Решение уравнения (38), удовлетворяющее краевым условиям (39), будем искать в виде
![]() , (40)
, (40)
где ![]() - решение
соответствующего однородного уравнения
- решение
соответствующего однородного уравнения
![]() , (41)
, (41)
а ![]() -
частное решение неоднородного уравнения
-
частное решение неоднородного уравнения
![]() . (42)
. (42)
Подставим (40) в первое условие граничной задачи 39), получим
![]() . (43)
. (43)
Для того,
чтобы равенство (43) было справедливо при любом с, необходимо и
достаточно, чтобы сомножитель ![]() =
0 и должны выполняться следующие равенства:
=
0 и должны выполняться следующие равенства:
![]() = 0, (44)
= 0, (44)
![]() . (45)
. (45)
Положим
![]() , (46)
, (46)
где постоянная k отлична от нуля.
Если ![]() , то
, то
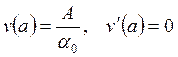 , (47)
, (47)
если ![]() , то
, то
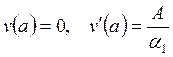 . (48)
. (48)
Видно, что ![]() является решением задачи Коши для
однородного уравнения (41), удовлетворяющим начальным условиям (46), а
является решением задачи Коши для
однородного уравнения (41), удовлетворяющим начальным условиям (46), а ![]() - решение задачи Коши для неоднородного
уравнения (42), удовлетворяющее начальным условиям (47) или (48).
- решение задачи Коши для неоднородного
уравнения (42), удовлетворяющее начальным условиям (47) или (48).
Теперь подставим (40) во второе условие граничной задачи (39) и выразим постоянную с
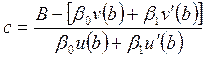 . (49)
. (49)
При этом
предполагается, что ![]() . Если выполнено
это условие, то краевая задача (38)-(39) имеет единственное решение, в
противном случае она или совсем не имеет решений, или их бесчисленное решение.
. Если выполнено
это условие, то краевая задача (38)-(39) имеет единственное решение, в
противном случае она или совсем не имеет решений, или их бесчисленное решение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.